【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
参考答案:
【答案】(1)证明见解析;(2)∠EOC的度数为40°;
(3)比值不变,∠OCB:∠OFB=1:2
(4)∠OCA的度数为60°.
【解析】试题分析:(1)根据等式性质及平行线的判定可以得到证明思路;
(2)根据角平分线及观察图形知道∠EOC=![]() ∠BOC=400;
∠BOC=400;
(3)∠OFB与∠OCB实际上是三角形的外角与不相邻的内角的关系,再观察图形可知两直线平行内错角相等,角平分线分得的两个角相等,等量代换可得结论;
(4)由∠OEB=∠OCA可以推出∠BOE=∠BCO=∠EOF=∠COF∠COA=200,从而∠OCA=600;
试题解析:
解:(1)∵BC∥OA,
∴∠B+∠O=180°,又∵∠B=∠A,
∴∠A+∠O=180°,
∴OB∥AC; 3分
(2)∵∠B+∠BOA=180°,∠B=100°,
∴∠BOA=80°,
∵OE平分∠BOF,
∴∠BOE=∠EOF,又∵∠FOC=∠AOC,
∴∠EOF+∠FOC= (∠BOF+∠FOA)= ∠BOA=40°;
(3)结论:∠OCB:∠OFB的值不发生变化.理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
(4)由(1)知:OB∥AC,
则∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
则∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEC=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=80°,
∴α=β=20°,
∴∠OCA=2α+β=40°+20°=60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y﹦(m+1)x+m2﹣1是正比例函数,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了 千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
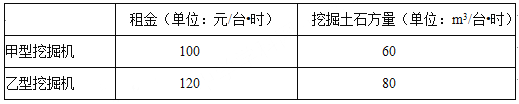
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2,直线y=x﹣2经过点C,交y轴于点G.

(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=x﹣2上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线顶点沿直线y=x﹣2平移,平移后的抛物线交y轴于点F,顶点为点E,求出当EF=EG时抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东营市某学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=﹣7x+4向下平移3个单位长度后得到的直线的表达式是( )
A. y=﹣7x+7 B. y=﹣7x+1 C. y=﹣7x﹣17 D. y=﹣7x+25
相关试题

