Question

【题目】菱形ABCD中，∠B＝60°，AB＝4，点E在BC上，CE＝2，若点P是菱形上异于点E的另一点，CE＝CP，则EP的长为_____．

Answer 1

【答案】6或2或3﹣．

【解析】

连接EP交AC于点H，依据菱形的性质可得到∠ECH=∠PCH=60°，然后依据SAS可证明△ECH≌△PCH，则∠EHC=∠PHC=90°，最后依据PE=EH求解即可.

解：如图所示：连接EP交AC于点H．

∵菱形ABCD中，∠B＝60°，

∴∠BCD＝120°，∠ECH＝∠PCH＝60°．

在△ECH和△PCH中 ，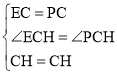

∴△ECH≌△PCH．

∴∠EHC＝∠PHC＝90°，EH＝PH．

∴OC=EC=.

∴EH=3,

∴EP＝2EH＝6．

如图2所示：当P在AD边上时，△ECP为等腰直角三角形，则 ．

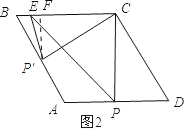
当P′在AB边上时，过点P′作P′F⊥BC．

∵P′C＝2，BC＝4，∠B＝60°，

∴P′C⊥AB．

∴∠BCP′＝30°．

∴ ．

∴ ．

故答案为6或2或3﹣．