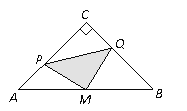
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为![]() ,△PMQ的面积为S (cm2),则S (cm2)与
,△PMQ的面积为S (cm2),则S (cm2)与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A. 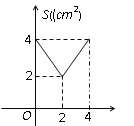 B.
B. 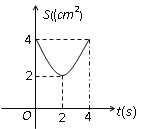 C.
C. 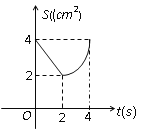 D.
D. 
参考答案:
【答案】B
【解析】当t=0时,点P与点A重合,点Q与点C重合,如图所示:
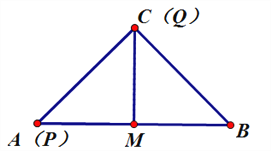
此时面积S△PMQ=![]() ;
;
当1<t≤2时,如图所示:
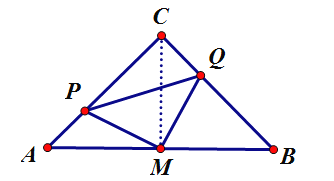
∵∠C=90°,AC=BC=4,
∴∠A=∠BCM=45°,MC=AM=![]() ,
,
又∵点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,
∴AP=CM=t
∴△APM≌△CQM(SAS)
∴S△PMQ=S△AMC- S△PCQ=4- ![]() =
=![]() ,
,
当t=2时,即点P、Q分别是AC、AB中点时,S△PMQ有最小值为2,
当t=4时,即点P与C重合,Q与B重合时,S△PMQ有最大值为4;
故选B。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣2a2)2a4﹣(﹣5a4)2
(2)4(a﹣b)2﹣(2a+b)(﹣b+2a)
(3)先化简,再求值:(3a+2)(3a﹣2)﹣8a(a﹣1)﹣(a﹣1)2 (其中:a=﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知⊙O为△ABC的外接圆,圆心O在AB上.
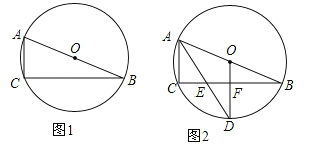
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的对角线AC、BD之比为3:4,其周长为40cm,则菱形ABCD的面积为cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=∠D=90°,AE平分∠BAD交CD于点E,过点C作CF∥AE交AB于点F. 求证:CF平分∠BCD.
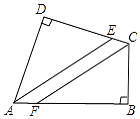
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于y的一元二次方程ky2﹣2y﹣1=0有两个不相等的实数根,则k的取值范围是( )
A. k>﹣1 B. k>﹣1且k≠0 C. k<1 D. k<1 且k≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+2=0根的情况是( )
A. 没有实数根 B. 只有一个实数根 C. 有两个相等的实数根 D. 有两个不相等的实数根
相关试题

