【题目】如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4 , 则S1+S2+S3+S4= . 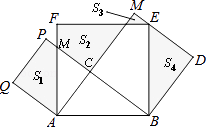
参考答案:
【答案】18
【解析】解:过F作AM的垂线交AM于N, 则Rt△ANF≌Rt△ABC,Rt△NFK≌Rt△CAT,
所以S2=SRt△ABC .
由Rt△NFK≌Rt△CAT可得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT ,
可得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC .
∵Rt△ABC≌Rt△EBD,
∴S4=SRt△ABC
∴S1+S2+S3+S4
=(S1+S3)+S2+S4
=SRt△ABC+SRt△ABC+SRt△ABC
=SRt△ABC×3
=4×3÷2×3
=18.
所以答案是:18.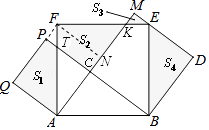
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有如下4个命题:①过两点可以作无数个圆.②三点可以确定一个圆.③任意一个三角形有且只有一个外接圆.④任意一个圆有且只有一个内接三角形.其中正确的有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
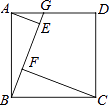
查看答案和解析>>【题目】如图,G为正方形ABCD的边AD上的一个动点,AE⊥BG,CF⊥BG,垂足分别为点E,F.已知AD=4,则AE2+CF2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组
频数
频率
49.5~59.5
0.08
59.5~69.5
0.12
69.5~79.5
20
79.5~89.5
32
89.5~100.5
a
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在一次适应性考试中,分数落在130﹣140分数段的人数为18人,频率为0.3,则该班共有_____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达204000米/分,这个数用科学记数法表示,正确的是( )
A.204×103
B.20.4×104
C.2.04×105
D.2.04×106 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向上平移3个单位后,得到△A1B1C1,请画出△A1B1C1,并直接写出点A1的坐标.
(2)将△ABC绕点O顺时针旋转90°,请画出旋转后的△A2B2C2,并求点B所经过的路径长(结果保留π)

相关试题

