【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
参考答案:
【答案】(1)工程队在使用新设备后每天能修路45米.(2)当m=26,n=16时,修建这条公路的总费用最少,最少费用为816000元.
【解析】
试题分析:(1)设使用旧设备每天能修路x米,则使用新设备后每天能修路(1+50)x=1.5x(米),根据题意,列出方程![]() ,即可解答;
,即可解答;
(2)设修建这条公路的总费用为W元,则W=16000m+25000n,由30m+45n=1500,得到m=![]() ,则W=16000×
,则W=16000×![]() +25000n=800000+1000n,根据16≤n≤26,利用一次函数的增减性即可解答.
+25000n=800000+1000n,根据16≤n≤26,利用一次函数的增减性即可解答.
解:(1)设使用旧设备每天能修路x米,则使用新设备后每天能修路(1+50)x=1.5x(米),
根据题意得:![]() ,
,
解得:x=30,
当x=30时,1.5x≠0,
∴x=30是分式方程的解,
1.5x=45,
答:工程队在使用新设备后每天能修路45米.
(2)设修建这条公路的总费用为W元,
则W=16000m+25000n,
∵30m+45n=1500,
∴m=![]() ,
,
把m=![]() 代入W=16000m+25000n得;
代入W=16000m+25000n得;
W=16000×![]() +25000n=800000+1000n,
+25000n=800000+1000n,
∵k=1000>0,
∴W随n的增大而增大,
∵16≤n≤26,
∴当n=16时,W有最小值,最小值为;800000+16000=816000(元),
m=![]() =26,
=26,
答:当m=26,n=16时,修建这条公路的总费用最少,最少费用为816000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?( )
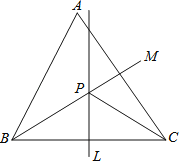
A.24° B.30° C.32° D.36°
-
科目: 来源: 题型:
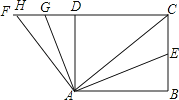
查看答案和解析>>【题目】如图,在矩形ABCD中,AC是对角线,点E是BC的中点,连接AE,AB=4,BC=3,将∠BAE绕点A逆时针旋转,使∠BAE的两边分别与线段CD的延长线相交于点G,H.当AH=AC时,CG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=
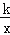 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )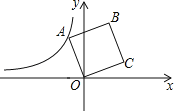
A.﹣2 B.﹣4 C.﹣
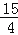 D.
D.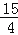
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OM⊥AB,NO⊥CD,∠1=
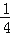 ∠BOC.
∠BOC.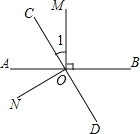
(1)求∠1的大小;
(2)求∠BON的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段中,能组成三角形的是( )
A. 3cm、4cm、8cm B. 3cm、5cm、8cm C. 5cm、6cm、10cm D. 5cm、6cm、11cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.

(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
相关试题

