【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A、B两种上网学习的月收费方案:
A方案:月租7元,可上网25小时,若超时,超出部分按每分钟0.01元收费;
B方案:月租10元,可上网50小时,若超时,超出部分按每分钟0.01元收费;
设每月上网学习时间为![]() 小时.
小时.
(1)当![]() >50时,用含有x的代数式分别表示A、B两种上网的费用;
>50时,用含有x的代数式分别表示A、B两种上网的费用;
(2)当x=100时,分别求出两种上网学习的费用.
(3)若上网40小时,选择哪种方式上网学习合算,为什么?
参考答案:
【答案】(1)方案A费用为: 0.01x+6.75,方案B费用为:0.01x+9.5.(2) 7.75, 10.5.(3) 选择A方式上网学习合算.
【解析】试题分析:(1)设每月上网学习时间为![]() 小时,根据A方案和B方案的要求列出代数式即可;(2)把x=100代入(1)中的代数式求值即可;(3)把x=40代入(1)中的代数式求值比较即可.
小时,根据A方案和B方案的要求列出代数式即可;(2)把x=100代入(1)中的代数式求值即可;(3)把x=40代入(1)中的代数式求值比较即可.
试题解析:
(1)方案A费用为: ![]() 0.01x+6.75.
0.01x+6.75.
方案B费用为:10+0.01(x-50)=0.01x+9.5.
(2)当x=100时,方案A费用为:0.01x+6.75=7.75.
方案B费用为: 0.01x+9.5=10.5.
(3)当x=40时,方案A费用为:0.01x+6.75=7.15.
方案B费用为:10.
∵7.15<10,
∴选择A方式上网学习合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了开展阳光体育运动,让学生每天能锻炼一小时,某学校去体育用品商店购买篮球与足球,篮球每只定价100元,足球每只定价50元.体育用品商店向学校提供两种优惠方案:①买一只篮球送一只足球;②篮球和足球都按定价的80%付款.现学校要到该体育用品商店购买篮球30只,足球x只(x>30).
(1)若该学校按方案①购买,篮球需付款 元,足球需付款 元(用含x的式子表示);
若该学校按方案②购买,篮球需付款 元,足球需付款 元(用含x的式子表示);
(2)若x=40,请通过计算说明按方案①、方案②哪种方案购买较为合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,垂足为
,垂足为 ,将线段
,将线段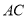 绕点
绕点 按逆时针方向旋转
按逆时针方向旋转 ,得到线段
,得到线段 ,连接
,连接 .
.
(1)线段
 ;
;(2)求线段
 的长度.
的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线与x轴交于点A(﹣
 , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣ ),求△ABN的面积s与t的函数解析式;
),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是个爱探究的学生,在学习完等腰三角形的判定定理之后,对于等腰
 (如图甲),若
(如图甲),若 ,
, ,小明发现,只要作
,小明发现,只要作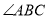 的平分线就可以将
的平分线就可以将 分成两个等腰三角形.
分成两个等腰三角形.(1)你认为小明的发现正确吗?若正确,请给出证明过程;若不正确,请说明理由;
(2)请你对图乙的三角形进行探索,将
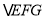 分成两个等腰三角形,并写出顶角度数;
分成两个等腰三角形,并写出顶角度数;(3)请你对图丙的三角形进行再探索,将
 分成三个等腰三角形,并写出顶角度数.
分成三个等腰三角形,并写出顶角度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离,即|x|=|x﹣0|,也就是说|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为:|x﹣y|表示在数轴上数x、y对应点之间的距离;在解题中,我们常常运用绝对值的几何意义.
①解方程|x|=2,容易看出,在数轴上与原点距离为2的点对应的数为±2,即该方程的解为x=±2.
②在方程|x﹣1|=2中,x的值就是数轴上到1的距离为2的点对应的数,显然x=3或x=﹣1.
③在方程|x﹣1|+|x+2|=5中,显然该方程表示数轴上与1和﹣2的距离之和为5 的点对应的x值,在数轴上1和﹣2的距离为3,满足方程的x的对应点在1的右边或﹣2的左边.若x的对应点在1的右边,由图示可知,x=2;同理,若x的对应点在﹣2的左边,可得x=﹣3,所以原方程的解是x=2或x=﹣3.根据上面的阅读材料,解答下列问题:
(1)方程|x|=5的解是_______________.
(2)方程|x﹣2|=3的解是_________________.
(3)画出图示,解方程|x﹣3|+|x+2|=9.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.

(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
相关试题

