Question

【题目】如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF.

(1)求证：BF=2AE；(2)若CD=1，求AD的长.

Answer 1

【答案】（1）证明见解析 （2）

【解析】

(1)先利用等腰直角三角形的性质及角的等量替换证明△ADC≌△BDF，得到BF=AC再根据等腰三角形三线合一得出AC=2AE，即可得证；

（2）在在Rt△CDF，利用勾股定理求出CF，再利用等腰三角形的性质得AF=CF，即可求出AD.

(1)证明：∵AD⊥BC，∠BAD=45°，

∴△ABD是等腰直角三角形，

∴AD=BD，

∵BE⊥AC，AD⊥BC，

∴∠CAD+∠ACD=90°，∠CBE+∠ACD=90°，

∴∠CAD=∠CBE，

在△ADC和△BDF中，，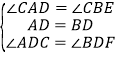

∴△ADC≌△BDF(ASA)，

∴BF=AC，

∵AB=BC，BE⊥AC，

∴AC=2AE，

∴BF=2AE；

(2)解：∵△ADC≌△BDF，

∴DF=CD=1，

在Rt△CDF中，CF=

∵BE⊥AC，AE=EC，

∴AF=CF=，

∴AD=AF+DF=1+.