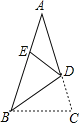
【题目】如图,△ABC中,AB=AC,点D为AC上一点,且BD=BC.将△BCD沿直线BD折叠后,点C落在AB上的点E处,若AE=DE,则∠A的度数为 .
参考答案:
【答案】36°.
【解析】
试题分析:设∠A=x°,由AE=DE,根据等腰三角形的性质,可求得∠ADE=x°,然后由三角形的外角的性质,求得∠AED=2x°,再利用折叠的性质与等腰三角形的性质,即可得∠C=∠BDC=2x°,∠CBD=x°,然后由三角形内角和定理,求得方程x+2x+2x=180,继而求得答案.
解:设∠A=x°,
∵AE=DE,
∴∠ADE=∠A=x°,
∴∠BEC=∠A+∠ADE=2x°,
由折叠的性质可得:∠C=∠BEC=2x°,
∵BD=BC,
∴∠BDC=∠C=2x°,
∴∠ABD=∠BDC﹣∠A=x°,
∴∠CBD=∠ABD=x°,
在△BCD中,∠C+∠CBD+∠BDC=180°,
∴x+2x+2x=180,
解得:x=36,
∴∠A=36°.
故答案为:36°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形
几何点数
层数
三角形数
正方形数
五边形数
六边形数




第一层几何点数
1
1
1
1
第二层几何点数
2
3
4
5
第三层几何点数
3
5
7
9
…
…
…
…
…
第六层几何点数
…
…
…
…
…
第n层几何点数
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三地的海拔高度分别为20米、-5米、和-10米,那么最高的地方比最低的地方高 米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A(1,3),B(2,4),C(3,5),D(4,6)其中不与E(2,-3)在同一个函数图像上的一个点是( )
A. 点A B. 点B C. 点C D. 点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 根据上述信息,解答下列问题:

(1)本次抽取的学生人数是 ______ ;扇形统计图中的圆心角α等于 ______ ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(﹣10,0),B(﹣6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.
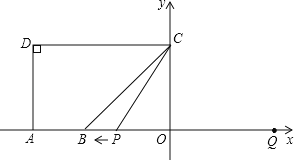
(1)求点C的坐标;
(2)当∠BCP=15°,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生家长对孩子使用手机的态度情况,随机抽取部分学生家长进行问卷调查,发出问卷140份,每位学生家长1份,每份问卷仅表明一种态度,将回收的问卷进行整理(假设回收的问卷都有效),并绘制了如图两幅不完整的统计图.
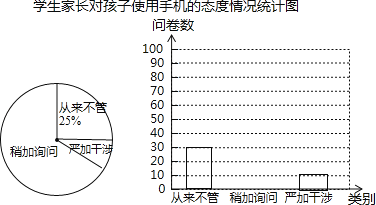
根据以上信息解答下列问题:
(1)回收的问卷数为 份,“严加干涉”部分对应扇形的圆心角度数为 .
(2)把条形统计图补充完整
(3)若将“稍加询问”和“从来不管”视为“管理不严”,已知全校共1500名学生,请估计该校对孩子使用手机“管理不严”的家长大约有多少人?
相关试题

