【题目】“五水共治”是浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水的大规模治水行动.五水共治,治污先行。市政府决定用96万元钱购买处理污水设备.现有A,B两种型号的处理污水设备,其中每台的价格、月处理污水量如下表.
A型 | B型 | |
价格(万元/台) | 8 | 6 |
月处理污水量(吨/台) | 120 | 100 |
(1)设A、B型设备应各买入x、y台,请你列出方程或方程组;
(2)用含y的代数式表示x,并写出所有满足题意的x,y的值;
(3)为了使月处理污水量达到最大,A,B型设备应各买多少台?最大月处理污水量为多少吨?
参考答案:
【答案】(1)8x+6y=96(2)![]() (3)最大月处理污水量为1600吨
(3)最大月处理污水量为1600吨
【解析】试题分析:(1)运用A型机器的单价×A型机器的数量+B型机器的单价×B型机器的数量就可以得出=总价96万元建立方程就可以了;(2)先移项,将不含x的项移到等号的右边,再将x的系数化为1,再根据x、y为自然数就可以满足条件的x、y的值;(3)计算出每种方案处理的污水吨数,再比较即可得出结论.
试题解析:(1)![]()
![]() 由
由![]() 得
得![]() ,
,
∵x、y是自然数,
∴![]()
(3)120×12=1440(吨)
120×9+100×4=1480(吨)
120×6+100×8=1520(吨)
④120×3+100×12=1560(吨)
⑤100×16=1600(吨)
![]() 1440<1480<1520<1560<1600
1440<1480<1520<1560<1600
![]() 为了使月处理污水量达到最大,应选择购买A型0台,B型16台;
为了使月处理污水量达到最大,应选择购买A型0台,B型16台;
最大月处理污水量为1600吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标中,点M(-2,3)在_______象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程组:
(1)
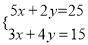 ;(2)
;(2)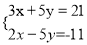 ;
;(3)
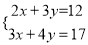 (4)
(4)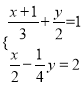
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为
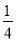 ;④
;④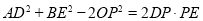 ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .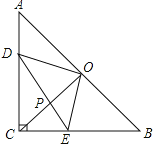
-
科目: 来源: 题型:
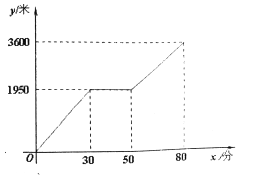
查看答案和解析>>【题目】小颖和小亮上山游玩,小颗乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颗在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米。图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从M地到N地有一条普通公路,总路程为120km;有一条高速公路,总路程为126km.甲车和乙车同时从M地开往N地,甲车全程走普通公路,乙车先行驶了另一段普通公路,然后再上高速公路.假设两车在普通公路和高速公路上分别保持匀速行驶,其中在普通公路上的行车速度为60km/h,在高速公路上的行车速度为100km/h.设两车出发x h时,距N地的路程为y km,图中的线段AB与折线ACD分别表示甲车与乙车的y与x之间的函数关系.
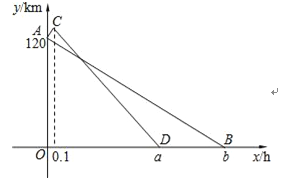
(1)填空:a= ,b= ;
(2)求线段AB、CD所表示的y与x之间的函数关系式;
(3)两车在何时间段内离N地的路程之差达到或超过30km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,a、b、c是直线,下列说法正确的是( )
A. 若a∥b,b∥c 则 a∥c
B. 若a⊥b,b⊥c,则a⊥c
C. 若a∥b,b⊥c,则a∥c
D. 若a∥b,b∥c,则a⊥c
相关试题

