【题目】抛物线y=﹣x2+(m﹣1)x+m与y轴交于(0,3)点
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标,与y轴交点坐标;
(3)画出这条抛物线;
(4)根据图象回答:①当x取什么值时,y>0,y<0?②当x取什么值时,y的值随x的增大而减小? 
参考答案:
【答案】
(1)解:∵抛物线y=﹣x2+(m﹣1)x+m与y轴交于(0,3)点,
∴m=3,
∴抛物线的解析式为y=﹣x2+2x+3
(2)解:令y=0,得x2﹣2x﹣3=0,
解得x=﹣1或3,
∴抛物线与x轴的交点坐标(﹣1,0),(3,0);
令x=0,得y=3,
∴抛物线与y轴的交点坐标(0,3)
(3)解:对称轴为x=1,顶点坐标(1,4),图象如图
(4)解:如图,①当﹣1<x<3时,y>0;
当x<﹣1或x>3时,y<0;
②当x>1时,y的值随x的增大而减小.
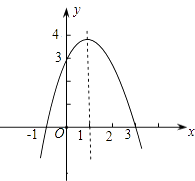
【解析】(1)将(0,3)代入y=﹣x2+(m﹣1)x+m求得m,即可得出抛物线的解析式;(2)令y=0,求得与x轴的交点坐标;令x=0,求得与y轴的交点坐标;(3)得出对称轴,顶点坐标,画出图象即可;(4)当y>0时,即图象在一、二象限内的部分;当y<0时,即图象在一、二象限内的部分;在对称轴的右侧,y的值随x的增大而减小.
【考点精析】本题主要考查了二次函数的图象和抛物线与坐标轴的交点的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是矩形纸片,翻折∠B,∠D,使AD,BC边与对角线AC重叠,且顶点B,D恰好落在同一点O上,折痕分别是CE,AF,则
 等于( )
等于( )
A.
 B. 2 C. 1.5 D.
B. 2 C. 1.5 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2017年杭州市某月24日08时至25日07时的空气质量指数统计图(空气质量指数AQI的值在不同的区间,就代表了不同的空气质量水平.比如0~50之间,代表“良好”,对应的颜色为绿色;51~100之间,代表“中等”,对应的颜色为黄色;101~150之间,代表“对敏感人群不健康”,对应的颜色为橙色,等等),则根据统计图得出的下列判断,正确的是( )

A. 在这个24小时中,AQI的值超过良好限值时段是24日08时至24日12时
B. 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上
C. 在这个24小时中,AQI的最大值和最小值的差为77
D. 建议中老年朋友在25日06时至07时进行晨练
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,则满足下列条件但不是直角三角形的是( )
A. ∠A=∠B-∠C B. ∠A:∠B:∠C=1:3:4 C. a:b:c=1:
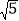 :3 D.
:3 D. 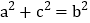
-
科目: 来源: 题型:
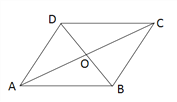
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=12,DO=OB=5,AC=26,∠ADB=90°.求BC的长和四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF=
 BC连接CD和EF.
BC连接CD和EF.(1)求证:DE=CF;
(2)求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°D为AB边上一点.
求证:(1)△ACE
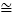 △BCD;
△BCD;(2)


相关试题

