【题目】如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=EF,AC=BD.求证:△ACF≌△BDE.

参考答案:
【答案】见解析
【解析】试题分析:先用HL证明Rt△ACE≌Rt△BDF,再利用公共边求出AF=BE,最后用SAS证明△ACF≌△BDE.
试题解析:
证明:∵AC⊥CE,BD⊥DF(已知),
∴∠ACE=∠BDF=90°(垂直的定义),
在Rt△ACE和Rt△BDF中,
AE=BF,AC=BD,
∴Rt△ACE≌Rt△BDF(HL),
∴∠A=∠B(全等三角形的对应角相等),
∵AE=BF(已知),
∴AE﹣EF=BF﹣EF(等式性质),
即AF=BE,
在△ACF和△BDE中,
AF=BE,∠A=∠B,AC=BD,
∴△ACF≌△BDE(SAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,外角∠EAB,∠ABF的平分线AD、BD相交于点D,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+1与y轴交于A点,与反比例函数
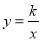 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且 .
.(1)求k的值;
(2)设点N(1,a)是反比例函数
 (x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在y轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣3x+k﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)选一个适当的k值使得此一元二次方程的根都是整数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 ,(k为常数,k≠1).
,(k为常数,k≠1).(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2x2﹣3x﹣3=0.(配方法) (2)2x2﹣7x+4=0.(公式法)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米.
(1)若墙长为18米,要围成鸡场的面积为150平方米,则鸡场的长和宽各为多少米?
(2)围成鸡场的面积可能达到200平方米吗?

相关试题

