搜索
【题目】下列运算中，正确的是( )
A. 7a＋a＝7a2 B. a2·a3＝a6 C. a3÷a＝a2 D. (ab)2＝ab2
参考答案：
【答案】C
【解析】
结合选项根据幂的乘方与积的乘方、同底数幂的乘法等知识点进行求解即可．
A. 7a＋a＝8a≠7a2，本选项错误；
B. a2·a3＝a5≠a6，本选项错误；
C. a3÷a＝a2，本选项正确；
D. (ab)2＝a2b2≠ab2，本选项错误.
故选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】将抛物线y=x2+4x向下平移3个单位，所得抛物线的表达式是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△A′B′C′是△ABC平移后得到的，若△ABC三个顶点的坐标分别为A(－2，3)，B(－4，－1)，C(2，0)，经过平移后A′的坐标为(3，6)，求相应的B′，C′的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠A＝50°，∠B－∠C＝70°，请按角的分类判断△ABC的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数
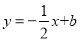（b为常数）的图象与x轴交于点A（2，0），与y轴交于点B，与反比例函数
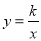的图象交于点C（-2，m）.（1）求点C的坐标及反比例函数的表达式；
（2）过点C的直线与y轴交于点D，且
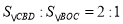，求点D的坐标. -
科目： 来源： 题型：
查看答案和解析>>【题目】【阅读理解】
我们知道，1+2+3+…+n=
，那么12+22+32+…+n2结果等于多少呢？在图1所示三角形数阵中，第1行圆圈中的数为1，即12，第2行两个圆圈中数的和为2+2，即22，…；第n行n个圆圈中数的和为
，即n2，这样，该三角形数阵中共有
个圆圈，所有圆圈中数的和为12+22+32+…+n2．
【规律探究】
将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n﹣1行的第一个圆圈中的数分别为n﹣1，2，n），发现每个位置上三个圆圈中数的和均为 ，由此可得，这三个三角形数阵所有圆圈中数的总和为：3（12+22+32+…+n2）= ，因此，12+22+32+…+n2= ．
【解决问题】
根据以上发现，计算：
的结果为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数y＝﹣（x﹣1）2+2有（ ）
A.最大值1B.最大值2C.最小值1D.最小值2
相关试题
