【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CDOE;
(3)若![]() ,求OE的长.
,求OE的长.

参考答案:
【答案】(1)DE为⊙O的切线,理由见解析
(2)证明见解析
(3)OE=![]()
【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;
(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;
(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.
试题解析:(1)DE为⊙O的切线,理由如下:
连接OD,BD,

∵AB为⊙O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE=![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,
∴∠C+∠A=90°,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴![]() ,即BC2=ACCD.
,即BC2=ACCD.
∴BC2=2CDOE;
(3)解:∵cos∠BAD=![]() ,
,
∴sin∠BAC=![]() ,
,
又∵BE=![]() ,E是BC的中点,即BC=
,E是BC的中点,即BC=![]() ,
,
∴AC=![]() .
.
又∵AC=2OE,
∴OE=![]() AC=
AC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式6x3﹣11x2+x+4可分解为
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某校有一块四边形空地ABCD如图,现计划在该空地上种草皮,经测量∠A=90°,AB=3cm,BC=12cm,CD=13cm,DA=4cm.若种每平方米草皮需100元,问需投入多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣m(m+x)(x﹣n)+mn(m﹣x)(n﹣x)的公因式是( )
A.﹣m
B.m(n﹣x)
C.m(m﹣x)
D.(m+x)(x﹣n) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知B(2,1),AB∥y轴,且AB=4,则A的坐标是( )
A. (2,-3)B. (2,5)C. (2,-3)或(2,5)D. (6,1)或(-2,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题一定成立的是 ( )
①对顶角相等; ②同位角相等,两直线平行;③全等三角形的周长相等;④面积相等的两个三角形全等
A. ①②③ B. ①④ C. ②④ D. ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并解答问题.
材料:将分式
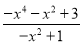 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴
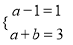 ,∴a=2,b=1
,∴a=2,b=1∴
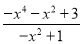 =
=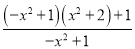 =
=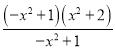 +
+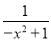 =x2+2+
=x2+2+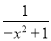 这样,分式
这样,分式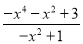 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式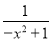 的和.
的和.解答:
(1)将分式
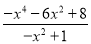 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.(2)试说明
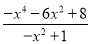 的最小值为8.
的最小值为8.
相关试题

