【题目】如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD
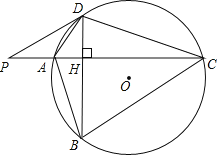
(1) 试判断PD与⊙O的位置关系,并说明理由
(2) 若tan∠ADB=![]() ,PA=
,PA=![]() AH,求BD的长
AH,求BD的长
参考答案:
【答案】(1)PD与圆O相切.理由见解析;(2)25![]()
【解析】
试题分析:(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;
(2)首先由tan∠ADB=![]() ,可设AH=3k,则DH=4k,又由PA=
,可设AH=3k,则DH=4k,又由PA=![]() AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE
AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE![]() cos30°=25
cos30°=25![]()
试题解析:(1)PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,

∵DE是直径,
∴∠DAE=90°,
∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,
∴∠PDA+∠ADE=90°,
即PD⊥DO,
∴PD与圆O相切于点D;
(2)∵tan∠ADB=![]()
∴可设AH=3k,则DH=4k,
∵PA=![]() AH,
AH,
∴PA=(4![]() -3)k,
-3)k,
∴PH=4![]() k,
k,
∴在Rt△PDH中,tan∠P=![]() ,
,
∴∠P=30°,∠PDH=60°,
∵PD⊥DO,
∴∠BDE=90°-∠PDH=30°,
连接BE,则∠DBE=90°,DE=2r=50,
∴BD=DE![]() cos30°=25
cos30°=25![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意实数a、b,定义一种运算:a※b=ab﹣a+b﹣2.例如,2※5=2×5﹣2+5﹣2=11.请根据上述的定义解决问题:若不等式1※x<2,则不等式的非负整数解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我校一块边长为2x米的正方形空地是八年级1﹣4班的卫生区,学校把它分成大小不同的四块,采用抽签的方式安排卫生区,下图是四个班级所抽到的卫生区情况,其中1班的卫生区是一块边长为(x﹣2y)米的正方形,其中0<2y<x.
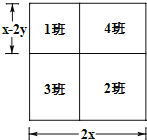
(1)分别用x、y的式子表示八年3班和八年4班的卫生区的面积;
(2)求2班的卫生区的面积比1班的卫生区的面积多多少平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校新到一批理、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务.
(1)王师傅单独整理这批实验器材需要多少分钟?
(2)学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
﹣(3a2﹣4ab)+[a2﹣2(2a+2ab)],其中a=﹣2,b=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画一条线段的垂线,垂足在( )
A. 线段上 B. 线段的端点
C. 线段的延长线上 D. 以上都有可能
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+y2)(x2+y2﹣1)=12,则x2+y2的值是 .
相关试题

