【题目】D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
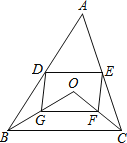
(1)如图,当点O在△ABC的内部时,求证:四边形DGFE是平行四边形;
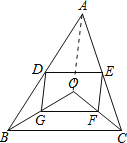
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?为什么?
(3)当OA与BC满足 时,四边形DGEF是一个矩形(直接填答案,不需证明.)
参考答案:
【答案】(1)见解析;(2)AO=BC;(3)OA⊥BC.
【解析】
试题分析:(1)首先利用三角形中位线的性质得出DE∥BC,DE=![]() BC,同理,GF∥BC,GF=
BC,同理,GF∥BC,GF=![]() BC,即可得出DE∥GF,DE=GF即可得出四边形DGFE是平行四边形;
BC,即可得出DE∥GF,DE=GF即可得出四边形DGFE是平行四边形;
(2)利用(1)中所求,只要邻边再相等即可得出答案.
(3)利用(1)中所求,只要邻边相互垂直的平行四边形即为矩形.
(1)证明:∵D、E分别是边AB、AC的中点.
∴DE∥BC,DE=![]() BC.
BC.
同理,GF∥BC,GF=![]() BC.
BC.
∴DE∥GF,DE=GF.
∴四边形DEFG是平行四边形.
(2)解:解法一:点O的位置满足两个要求:AO=BC,且点O不在射线CD、射线BE上.
∵由(1)得出四边形DEFG是平行四边形,
∴点O的位置满足两个要求:AO=BC,且点O不在射线CD、射线BE上时,
可得GD=![]() AO,GF=
AO,GF=![]() BC,
BC,
∴DG=GE,
∴平行四边形DEFG是菱形;
解法二:点O在以A为圆心,BC为半径的一个圆上,但不包括射线CD、射线BE与⊙A的交点.
解法三:过点A作BC的平行线l,点O在以A为圆心,BC为半径的一个圆上,但不包括l与⊙A的两个交点.
(3)由(1)知,四边形DEFG是平行四边形.
当OA⊥BC时,DG⊥GF,
故平行四边形DGFE是矩形.
故答案是:OA⊥BC.
-
科目: 来源: 题型:
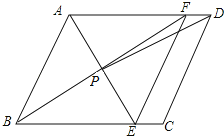
查看答案和解析>>【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD,若AB=4,AD=6,∠ABC=60°,PD的长 ,四边形ABEF的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:
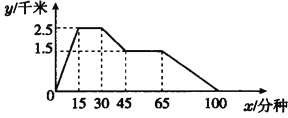
(1)体育场离小明家多远?小明从家到体育场用了多少时间?
(2)体育场离文具店多远?
(3)小明在文具店逗留了多少时间?
(4)小明从文具店回家的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
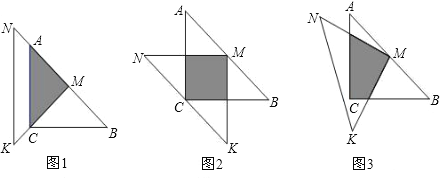
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
-
科目: 来源: 题型:
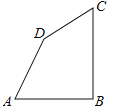
查看答案和解析>>【题目】如图、四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,已知四边形的周长为30,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x﹣5与2x﹣1的值相等,则x的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a+2a=5a2 B. 3a+3b=3ab C. 2a2bc-a2bc=a2bc D. a5-a2=a3
相关试题

