【题目】动手实验:利用矩形纸片(如图1)剪出一个正六边形纸片;再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形) ,如图2.

(1) 做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2) 在(1)的条件下,当矩形的长为2a时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率为多少?
![]()
参考答案:
【答案】(1)、2:![]() ;(2)、
;(2)、![]()
【解析】
试题分析:(1)、首先根据题意画出图形,然后分别求出矩形的长和宽与正六边形半径长的关系,得出比值;(2)、分别求出正六棱柱和矩形纸片的面积,然后得出比值.
试题解析:(1)如图所示:

由于正六边形内角和为(6﹣2)×180°=720°,则其一角的角平分线所分的两个角同为60°;
设所需矩形的长宽分别为A、B,剪出的正六边形半径长为L,那么
A=2L,B=2L![]() sin60°=
sin60°=![]() L;
L;
因此,所求长宽比为A:B=(2L):(![]() L)=2:
L)=2:![]() .
.
做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为:2:![]() ;
;
(2)∵矩形的长为2a, ∴正六边形边长为a,其面积为:设高为x,S=![]()
当x=![]() 时,S=
时,S=![]() , 此时,底面积
, 此时,底面积![]() ,
,
∴六棱柱的面积为![]() +
+![]() =
=![]()
∵矩形的面积=![]() ,
,
∴利用率= =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,M 是AB的中点,且AN=
 AD,问△CMN是什么三角形?并加以证明。
AD,问△CMN是什么三角形?并加以证明。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形的一边AD,使点D 落在BC边上的点F处, BC=15cm,AB=9cm
求(1)FC的长;(2)EF的长.

-
科目: 来源: 题型:
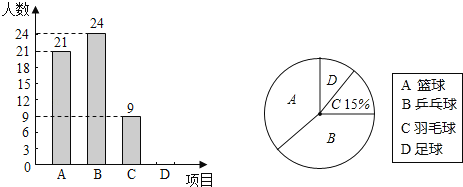
查看答案和解析>>【题目】某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:
(1)这次被抽查的学生有 人;请补全条形统计图;
(2)在统计图2中,“乒乓球”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. x=-1是方程4x+3=0的解
B. m=-1是方程9m+4m=13的解
C. x=1是方程3x-2=3的解
D. x=0是方程0.5(x+3)=1.5的解
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,﹣3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个在三视图中俯视图与主视图完全相同的几何体 .
相关试题

