【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点. 
(1)求出A点坐标及直线l2的解析式;
(2)连接BC,求出S△ABC .
参考答案:
【答案】
(1)解:∵A点在直线l1上,且横坐标为﹣1,
∴y1=2×(﹣1)+3=1,即A点的坐标为(﹣1,1)
又直线l2过A点,将(﹣1,1)代入直线l2解析式得:1=﹣k﹣1,k=﹣2,
则直线l2的解析式为:y2=﹣2x﹣1
(2)解:l1与x轴交于B点,则B点坐标为( ![]() ),l1与y轴交于D点,
),l1与y轴交于D点,
则D点坐标为(0,3),l2与y轴交于C点,则C点坐标为(0,﹣1),
S△ABC=S△BCD﹣S△ACD= ![]() CD|xB|﹣
CD|xB|﹣ ![]() CD|xA|=1
CD|xA|=1
【解析】(1)根据A点在直线l1上,且横坐标为﹣1,求出A点的坐标,再根据直线l2过A点,将(﹣1,1)代入直线l2解析式,即可求出答案;(2)根据已知得出B点的坐标,再根据l1与y轴交于D点,得出D点和C点的坐标,再根据三角形的面积公式得出S△ABC .
【考点精析】本题主要考查了确定一次函数的表达式和三角形的面积的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
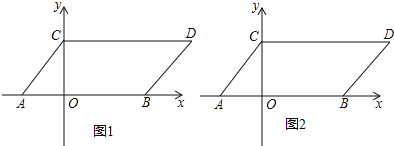
(1)写出点C,D的坐标并求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由;
(3)如图2,点P是直线BD上的一个动点,连接PC,PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD,∠POB的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从
 ,
,  两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经
两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经 小时两人相遇.已知在相遇时乙比甲多行驶了
小时两人相遇.已知在相遇时乙比甲多行驶了 千米,且摩托车的速度是自行车速度的
千米,且摩托车的速度是自行车速度的 倍.
倍.(1)问甲、乙行驶的速度分别是多少?
(2)甲、乙行驶多少小时,两车相距
 千米?
千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】5的相反数的平方是__,﹣1的倒数是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣(﹣5)2__﹣|﹣62|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于抛物线y=2x2﹣3的说法,正确的是( )
A.抛物线的开口向下
B.抛物线的对称轴是直线x=1
C.抛物线与x轴有两个交点
D.抛物线y=2x2﹣3向左平移两个单位长度可得抛物线y=2(x﹣2)2﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.问四边形AFCE是菱形吗?请说明理由.

相关试题

