【题目】甲、乙两人从![]() ,
, ![]() 两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经
两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经![]() 小时两人相遇.已知在相遇时乙比甲多行驶了
小时两人相遇.已知在相遇时乙比甲多行驶了![]() 千米,且摩托车的速度是自行车速度的
千米,且摩托车的速度是自行车速度的![]() 倍.
倍.
(1)问甲、乙行驶的速度分别是多少?
(2)甲、乙行驶多少小时,两车相距![]() 千米?
千米?
参考答案:
【答案】(1) 甲、乙行驶的速度分别是每小时15千米、45千米;(2) 甲、乙行驶![]() 或
或![]() 小时,两车相距30千米
小时,两车相距30千米
【解析】试题分析:
(1)设甲行驶的速度为每小时![]() 千米,可得乙行驶的速度为每小时
千米,可得乙行驶的速度为每小时![]() 千米,则相遇时甲行驶路程为
千米,则相遇时甲行驶路程为![]() 千米,乙行驶路程为
千米,乙行驶路程为![]() 千米,根据相遇时,乙比甲多行驶90千米即可列出方程,解方程即可求得两人的速度;
千米,根据相遇时,乙比甲多行驶90千米即可列出方程,解方程即可求得两人的速度;
(2)根据(1)小题求得的结果,可知A、B两地相距180千米,根据题意当两人相距30千米时,两人行驶的路程之和为(180-30)或(180+30),由此设两人行驶![]() 小时后相距30千米,分两种情况列出方程,解方程即可得到所求答案.
小时后相距30千米,分两种情况列出方程,解方程即可得到所求答案.
试题解析:
(1)设甲行驶的速度是每小时![]() 千米,根据题意,得:
千米,根据题意,得:
![]() ,解得:
,解得: ![]() ,
,
∴甲、乙行驶的速度分别是每小时15千米、45千米;
(2)由第(1)小题,可得A,B两地相距45×3+15×3=180(千米).
设甲、乙行驶![]() 小时后,两车相距30千米,根据题意可得两车行驶的总路程是(180-30)千米或(180+30)千米,则:
小时后,两车相距30千米,根据题意可得两车行驶的总路程是(180-30)千米或(180+30)千米,则:
![]() 或
或![]() .
.
解得: ![]() 或
或![]() .
.
∴甲、乙行驶![]() 或
或![]() 小时,两车相距30千米.
小时,两车相距30千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
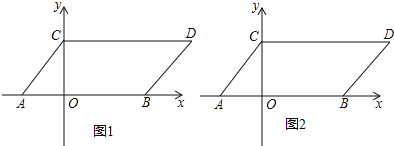
(1)写出点C,D的坐标并求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由;
(3)如图2,点P是直线BD上的一个动点,连接PC,PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD,∠POB的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】5的相反数的平方是__,﹣1的倒数是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.

(1)求出A点坐标及直线l2的解析式;
(2)连接BC,求出S△ABC . -
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:﹣(﹣5)2__﹣|﹣62|.
相关试题

