【题目】如图,是将抛物线y=﹣x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C.
(1)求抛物线的函数表达式;
(2)若点N为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y= ![]() x+
x+ ![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P,Q的坐标;若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P,Q的坐标;若不存在,说明理由.
参考答案:
【答案】
(1)
解:设抛物线的解析式是y=﹣(x﹣1)2+k.
把(﹣1,0)代入得0=﹣(﹣1﹣1)2+k,
解得k=4,
则抛物线的解析式是y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)
解:在y=﹣x2+2x+3中令x=0,则y=3,即C的坐标是(0,3),OC=3.
∵B的坐标是(3,0),
∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形.
∴∠OCB=45°,
过点N作NH⊥y轴,垂足是H.
∵∠NCB=90°,
∴∠NCH=45°,
∴NH=CH,
∴HO=OC+CH=3+CH=3+NH,
设点N纵坐标是(a,﹣a2+2a+3).
∴a+3=﹣a2+2a+3,
解得a=0(舍去)或a=1,
∴N的坐标是(1,4);
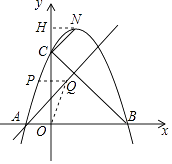
(3)
解:∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,﹣t2+2t+3),代入y= ![]() x+
x+ ![]() ,则﹣t2+2t+3=
,则﹣t2+2t+3= ![]() (t+1)+
(t+1)+ ![]() ,
,
整理,得2t2﹣t=0,
解得t=0或 ![]() .
.
∴﹣t2+2t+3的值为3或 ![]() .
.
∴P、Q的坐标是(0,3),(1,3)或( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() ).
).
【解析】(1)已知抛物线的对称轴,因而可以设出顶点式,利用待定系数法求函数解析式;(2)首先求得B和C的坐标,易证△OBC是等腰直角三角形,过点N作NH⊥y轴,垂足是H,设点N纵坐标是(a,﹣a2+2a+3),根据CH=NH即可列方程求解;(3)四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,设P(t,﹣t2+2t+3),代入y= ![]() x+
x+ ![]() ,即可求解.
,即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=
 ,OB=2
,OB=2  ,反比例函数y=
,反比例函数y=  的图象经过点B.
的图象经过点B.
(1)求反比例函数的表达式;
(2)若△AMB与△AOB关于直线AB对称,一次函数y=mx+n的图象过点M、A,求一次函数的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元,大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.

(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.

(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形?并证明你的结论(请先补全图形,再解答);
(3)若ED=EF,ED与EF垂直吗?若垂直给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算错误的是( )
A.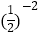 =4
=4
B.32×3﹣1=3
C.20÷2﹣2=
D.(﹣3×102)3=﹣2.7×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )

A.AB=AC
B.AD=BD
C.BE⊥AC
D.BE平分∠ABC
相关试题

