【题目】已知, ![]() ∥
∥![]() ,
, ![]() ,试解答下列问题:
,试解答下列问题:
(1)如图①,则![]() __________,则OB与AC的位置关系为__________
__________,则OB与AC的位置关系为__________

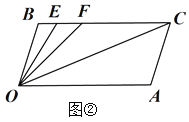
(2)如图②,若点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,并且
,并且![]() 平分
平分![]() .则
.则![]() 的度数等于_____________;
的度数等于_____________;
(3)在第(2)题的条件下,若平行移动![]() 到如图③所示位置.
到如图③所示位置.
①在AC移动的过程中, ![]() 与
与![]() 的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
②当∠OEB=∠OCA时,求∠OCA

参考答案:
【答案】(1)72°,平行;(2)36°;(3)①不变, ![]() 与
与![]() 的比值为
的比值为![]() ;②54°
;②54°
【解析】试题分析:(1)根据平行线的判定可以得到∠B+∠O=180°,再根据∠A=∠B可得∠A++∠O=180°,进而得证;
(2)根据角平分线及观察图形知道∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,进而得到∠EOC=
∠FOA,进而得到∠EOC=![]() (∠BOF-∠FOA)=
(∠BOF-∠FOA)=![]() ∠BOA,即可求解;
∠BOA,即可求解;
(3) ①由平行线的性质可求解;
②由①可根据平行公理的推论,可以推出结论.
试题解析:(1)72°,平行
(2)36°
(3)①不变
![]() ∥
∥![]()
又![]()
![]()
![]()
又![]()
![]() ∥
∥![]()
![]()
![]()
即![]() :
: ![]()
![]() :
:![]() .
.
![]() 与
与![]() 的比值为
的比值为![]()
②由(1)知:OB∥AC,∴∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
∴∠OCA=∠BOC=2α+β
由(1)知:BC∥OA,
∴∠OEB=∠EOA =α+β+β=α+2β
∵∠OEB=∠OCA
∴2α+β=α+2β
∴α=β
∵∠AOB=72°,
∴α=β=18°
∴∠OCA=2α+β=36°+18°=54°
-
科目: 来源: 题型:
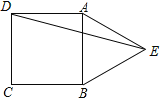
查看答案和解析>>【题目】如图,等边△ABE与正方形ABCD有一条共公边,点E在正方形外,连结DE,则∠BED= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15° .
(1)求证:△AOB为等边三角形;
(2)求∠BOE度数.

-
科目: 来源: 题型:
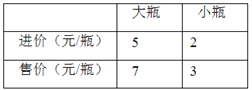
查看答案和解析>>【题目】已知某品牌的饮料有大瓶和小瓶装之分,某超市花了3800元购进一批该品牌的饮料共1000瓶,其中,大瓶和小瓶饮料的进价及售价如表所示.
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次购买大瓶饮料时,每满2瓶就送1瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
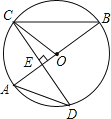
(1)求证:∠BCO=∠D;
(2)若CD=
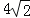 ,AE=2,求⊙O的半径.
,AE=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式x+2y的值是3,则代数式3x+6y+1的值是( )
A. 7 B. 4 C. 10 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形中顶角的度数是底角的3倍,那么底角的度数是____.
相关试题

