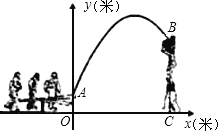
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=![]() x2+3x+1的一部分,如图所示.
x2+3x+1的一部分,如图所示.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
参考答案:
【答案】(1)、![]() 米;(2)、能成功,理由见解析.
米;(2)、能成功,理由见解析.
【解析】
试题分析:(1)、将二次函数转化成顶点式,从而得出最大值;(2)、将x=4代入函数解析式看函数值是否等于3.4,如果等于就是成功,不等于就是不成功.
试题解析:(1)、将二次函数y=![]() x2+3x+1化成y=
x2+3x+1化成y=![]() (x
(x![]() )2
)2![]() ,
,
当x=![]() 时,y有最大值,y最大值=
时,y有最大值,y最大值=![]() ,
,
因此,演员弹跳离地面的最大高度是4.75米.
(2)、能成功表演.理由是:
当x=4时,y=![]() ×42+3×4+1=3.4. 即点B(4,3.4)在抛物线y=
×42+3×4+1=3.4. 即点B(4,3.4)在抛物线y=![]() x2+3x+1上,
x2+3x+1上,
因此,能表演成功
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
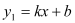 的图象与反比例函数
的图象与反比例函数 的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.(1)求反比例函数
 和一次函数
和一次函数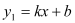 的解析式;(2)连结OA,OC,求△AOC的面积.
的解析式;(2)连结OA,OC,求△AOC的面积.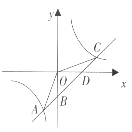
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D、E为垂足,BD与CE交于点O,则图中全等三角形共有_________对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把0.002048四舍五入保留两个有效数字得 , 它是精确到位的近似数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0.
相关试题

