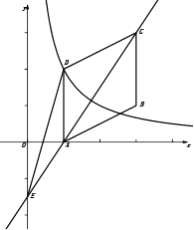
【题目】（本题满分10分）如图，在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），双曲线y=（k≠0，x＞0）过点D．

（1）求此双曲线的解析式；

（2）作直线AC交y轴于点E，连结DE，求△ CDE的面积．

参考答案：

【答案】（1）；（2）3．

【解析】试题分析：（1）根据在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），可以求得点D的坐标，又因为双曲线（k≠0，x＞0）过点D，从而可以求得k的值，从而可以求得双曲线的解析式；

（2）由图可知三角形CDE的面积等于三角形EDA与三角形ADC的面积之和，从而可以解答本题．

试题解析：（1）∵在平行四边形ABCD中，点A、B、C的坐标分别是（1，0）、（3，1）、（3，3），∴点D的坐标是（1，2），∵双曲线（k≠0，x＞0）过点D，∴2=，得k=2，即双曲线的解析式是： ；

（2）∵直线AC交y轴于点E，∴S△CDE=S△EDA+S△ADC==1+2=3，即△CDE的面积是3．

关闭