Question

【题目】如图，在△ABC中，∠ABC=90°，AB=CB，点E在边BC上，点F在边AB的延长线上，BE=BF．

（1）求证：△ABE≌△CBF；
（2）若∠CAE=30°，求∠ACF的度数．

Answer 1

【答案】
（1）证明：∵∠ABC=90°，

∴∠ABC=∠CBF=90°．

在△ABE和△CBF中，

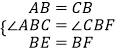
∴△ABE≌△CBF（SAS）

（2）解：∵△ABE≌△CBF，

∴∠BAE=∠BCF．

∵∠ABC=90°，AB=CB，

∴∠BCA=∠BAC=45°．

∵∠CAE=30°，

∴∠BAE=15°，

∴∠BCF=15°．

∵∠ACF=∠BCF+∠ACB，

∴∠ACF=15°+45°=60°．

答：∠ACF的度数为60°

【解析】（1）由∠ABC=90°就可以求出∠CBF=90°，由SAS就可以得出△ABE≌△CBF；（2）由∠CAE=30°就可以求出∠BAE=15°，就可以得出∠BCF=15°，由条件可以求出∠ACB=45°，进而可以求出∠ACF的度数．