【题目】如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4 ![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F 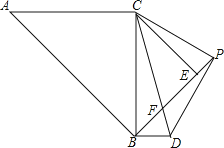
(1)求证: ![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
参考答案:
【答案】
(1)
证明:∵△BCE和△CDP均为等腰直角三角形,
∴∠ECB=∠PCD=45°,∠CEB=∠CPD=90°,
∴△BCE∽△DCP,
∴ ![]()
(2)
解:AC∥BD,
理由:∵∠PCE+∠ECD=∠BCD+∠ECD=45°,
∴∠PCE=∠BCD,
又∵ ![]() ,
,
∴△PCE∽△DCB,
∴∠CBD=∠CEP=90°,
∵∠ACB=90°,
∴∠ACB=∠CBD,
∴AC∥BD;
(3)
解:如图所示: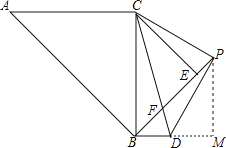
作PM⊥BD于M,
∵AC=4 ![]() ,△ABC和△BEC均为等腰直角三角形,
,△ABC和△BEC均为等腰直角三角形,
∴BE=CE=4,
∵△PCE∽△DCB,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴BD= ![]() x,
x,
∵∠PBM=∠CBD﹣∠CBP=45°,BP=BE+PE=4+x,
∴PM= ![]() ,
,
∴△PBD的面积S= ![]() BDPM=
BDPM= ![]() ×
× ![]() x×
x× ![]() =
= ![]() x2+2x.
x2+2x.
【解析】(1)直接利用相似三角形的判定方法得出△BCE∽△DCP,进而得出答案;
(2)首先得出△PCE∽△DCB,进而求出∠ACB=∠CBD,即可得出AC与BD的位置关系;
(3)首先利用相似三角形的性质表示出BD,PM的长,进而表示出△PBD的面积.此题主要考查了相似形综合、平行线的判定方法以及相似三角形的判定与性质等知识,正确表示出PM的长是解题关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
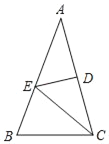
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )
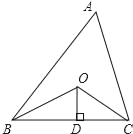
A. 20 B. 25 C. 30 D. 35
-
科目: 来源: 题型:
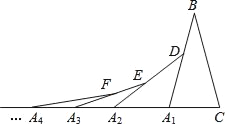
查看答案和解析>>【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,第2017个三角形的底角度数是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
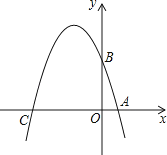
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值. -
科目: 来源: 题型:
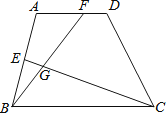
查看答案和解析>>【题目】如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( )
A.95
B.100
C.105
D.110
相关试题

