【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽![]() 米时,拱顶(拱桥洞的最高点)离水面
米时,拱顶(拱桥洞的最高点)离水面![]() ,水面上升
,水面上升![]() 时,水面的宽度为________.
时,水面的宽度为________.

参考答案:
【答案】![]()
【解析】
根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=1代入抛物线解析式得出水面宽度,即可得出答案.
建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
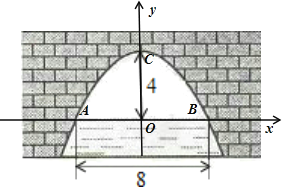
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半4米,抛物线顶点C坐标为(0,4),
通过以上条件可设顶点式y=ax2+4,其中a可通过代入A点坐标(-4,0)到抛物线解析式得出:a=-![]() ,
,
所以抛物线解析式为y=-![]() x2+4,
x2+4,
当水面上升1米,通过抛物线在图上的观察可转化为:
当y=1时,对应的抛物线上两点之间的距离,也就是直线y=1与抛物线相交的两点之间的距离,
可以通过把y=1代入抛物线解析式得出:
1=-![]() x2+4,
x2+4,
解得:x=±2![]() ,
,
所以水面宽度增加到4![]() 米,
米,
故答案为:4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,AP+BP+CP的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数
 的图象,下列结论中:①
的图象,下列结论中:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .正确的个数是( )
.正确的个数是( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线
 与
与 轴的交点为
轴的交点为 ,则下列说法不正确的是( )
,则下列说法不正确的是( )A. 抛物线开口向上
B. 抛物线的对称轴是

C. 当
 时,
时, 的最大值为
的最大值为
D. 抛物线与
 轴的交点为
轴的交点为 ,
,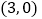
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
,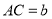 ,
, .设
.设 为最长边.当
为最长边.当 时,
时, 是直角三角形;当
是直角三角形;当 时,利用代数式
时,利用代数式 和
和 的大小关系,探究
的大小关系,探究 的形状(按角分类).
的形状(按角分类).(1)当
 三边分别为6、8、9时,
三边分别为6、8、9时, 为______三角形;当
为______三角形;当 三边分别为6、8、11时,
三边分别为6、8、11时, 为______三角形.
为______三角形.(2)猜想,当
 ______
______ 时,
时, 为锐角三角形;当
为锐角三角形;当 ______
______ 时,
时, 为钝角三角形.
为钝角三角形.(3)判断当
 ,
, 时,
时, 的形状,并求出对应的
的形状,并求出对应的 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
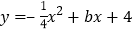 与
与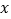 轴相交于
轴相交于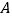 、
、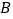 两点,与
两点,与 轴相交于点
轴相交于点 .若已知
.若已知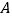 点的坐标为
点的坐标为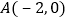 .点
.点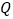 在抛物线的对称轴上,当
在抛物线的对称轴上,当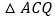 为等腰三角形时,点
为等腰三角形时,点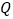 的坐标为________.
的坐标为________.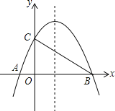
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题背景:在
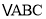 中,
中,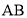 、
、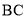 、
、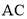 三边的长分别为
三边的长分别为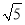 、
、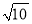 、
、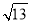 ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为 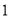 ),在网格中画出格点
),在网格中画出格点 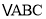 (即
(即 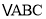 三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.
三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.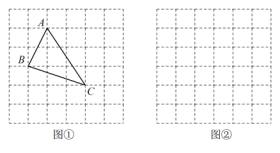
(1)请你直接写出
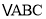 的面积为 .
的面积为 .(2)若
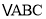 三边的长分别为
三边的长分别为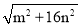 、
、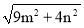 、
、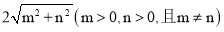 运用构图法求出这三角形的面积.
运用构图法求出这三角形的面积.
相关试题

