【题目】如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是( )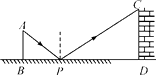
A.6米
B.8米
C.18米
D.24米
参考答案:
【答案】B
【解析】由题意知:光线AP与光线PC,∠APB=∠CPD,
∴Rt△ABP∽Rt△CDP,
∴ ![]() ,∴CD
,∴CD![]() (米).
(米).
故答案为:B
根据反射角等于入射角,及等角的余角相等得出∠APB=∠CPD,从而利用两角分别相等得两个三角形相似得出Rt△ABP∽Rt△CDP,根据相似三角形对应边成比例得出AB∶CD=BP∶PD ,从而得出关于CD的方程,求解得出CD的长度,即该古城墙的高度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个小正方形边长都为1个单位长度.

①画出将△ABC向下平移4个单位得到的△A1B1C1;
②画出△ABC关于原点O的中心对称图形△A2B2C2;
③画出△A1B1C1绕着点A1顺时针方向旋转90°后得到的△A3B3C3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2 , 并写出点A2、B2、C2坐标;
③请画出△ABC绕原点O逆时针旋转90°后△A3B3C3 , 并写出点A3、B3、C3坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)2a3(a2)3÷a
(3)(x﹣1)2﹣x(x+1)
(4)20002﹣1999×2001(用简便方法计算)
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成
 ,
, ,
, ,
, 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).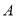 组:
组: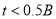 组:
组: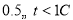 组:
组: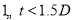 组:
组: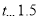

请根据上述信息解答下列问题:
(1)
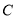 组的人数是 ;
组的人数是 ;(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 是
是 的中点,将
的中点,将 沿
沿 折叠后得到
折叠后得到 ,点
,点 在矩形
在矩形 内部,延长
内部,延长 交
交 于点G.
于点G.
(1)猜想线段
 与
与 有何数量关系?并证明你的结论;
有何数量关系?并证明你的结论;(2)若
 ,
, ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形
 中,
中, .
.
(1)如图1,点
 为线段
为线段 的中点,连接
的中点,连接 ,
, .若
.若 ,求线段
,求线段 的长.
的长.(2)如图2,
 为线段
为线段 上一点(不与
上一点(不与 ,
, 重合),以
重合),以 为边向上构造等边三角形
为边向上构造等边三角形 ,线段
,线段 与
与 交于点
交于点 ,连接
,连接 ,
, ,
, 为线段
为线段 的中点.连接
的中点.连接 ,
, 判断
判断 与
与 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.(3)在(2)的条件下,若
 ,请你直接写出
,请你直接写出 的最小值.
的最小值.
相关试题

