【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
![]()
当A、B两点都不在原点时,如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
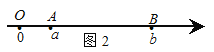
如图3,当点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
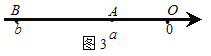
如图4,当点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= ![]() =∣a-b∣;
=∣a-b∣;
回答下列问题:
(1)数轴上表示1和6的两点之间的距离是 ,数轴上表示2和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-4,则点A和B之间的距离是 ,若∣AB∣=3,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数![]() ,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
参考答案:
【答案】(1)5 ;5(2)![]() ;-7或-1(3)-4或3(4)
;-7或-1(3)-4或3(4)![]() ;
;![]()
【解析】试题分析:
(1)由阅读材料内容可知:若数轴上任意两点A、B所表示的数分别为:a、b,则A、B两点间的距离![]() ,由此可计算本题答案;
,由此可计算本题答案;
(2)同(1)可解得第一空的答案;根据(1)中的公式和绝对值的意义,可列方程解得第二空的答案;
(3)由阅读材料可知:![]() 表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,我们分
表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,我们分![]() 、
、![]() 和
和![]() 三种情况来化简式子
三种情况来化简式子![]() 就可求得“x”的值;
就可求得“x”的值;
(4)由题意可知:点A表示的数为“-1”,点B表示的数是“9”,则由已知可得:![]() ,
,![]() ,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论,如图1和图2,列出方程可求解;
,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论,如图1和图2,列出方程可求解;
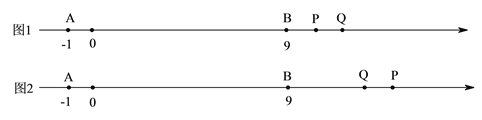
试题解析:
(1)∵![]() ,
,
∴两空都应填“5”;
(2)∵数轴上若点A表示的数是x,点B表示的数是-4,
∴![]() ;
;
又∵![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() 或
或![]() ;
;
(3)由阅读材料可知:![]() 表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,所以要我们分
表示在数轴上表示数“x”的点到表示数“-2”和数“1”这两个点的距离之和等于7,所以要我们分![]() 、
、![]() 和
和![]() 三种情况来讨论:
三种情况来讨论:
①当![]() 时,
时,![]() 可化为:
可化为:![]() ,解得:
,解得:![]() ;
;
②当![]() 时,
时,![]() 可化为:
可化为:![]() ,该式子不成立;
,该式子不成立;
③当![]() 时,
时,![]() 可化为:
可化为:![]() ,解得;
,解得;![]() ;
;
综上所述:![]() 或
或![]() ;
;
(4)由题意可知:点A表示的数为“-1”,点B表示的数是“9”,则由已知可得:
![]() ,
,![]() ,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论:
,当P与Q相距1个单位长度时,要分点Q在点P右边和点Q在点P左边两种情况来讨论:
①如图1,当Q在P的右边时,由![]() 可得:
可得:![]() ,即
,即![]() ,解得:
,解得:![]() ;
;
②如图2,当Q在P的左边时,由![]() 可得:
可得:![]() ,即
,即![]() ,解得
,解得![]() ;
;
综上所述:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为 米.(结果保留根号)
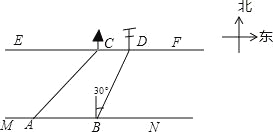
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学八年级学生到离学校15千米的青少年营地举行庆祝十四岁生日活动,先遣队与大部队同时从学校出发.已知先遣队每小时比大部队多行进1千米,预计比大部队早半小时到达目的地.求先遣队与大部队每小时各行进了多少千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】梅凯种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格将打折,并依此得到付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如图所示,下列四种说法:
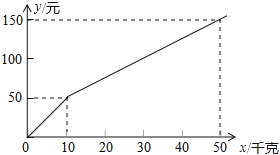
①一次购买种子数量不超过10千克时,销售价格为5元/千克;
②一次购买30千克种子时,付款金额为100元;
③一次购买10千克以上种子时,超过10千克的那部分种子的价格打五折;
④一次购买40千克种子比分两次购买且每次购买20千克种子少花25元钱.
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,
(1)求∠DEC的度数。
(2)直接写出图中所有的等腰三角形。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°
(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四种统计图:①条形图;②扇形图;③折线图;④直方图.四个特点:(a)易于比较数据之间的差异;(b)易于显示各组之间的频数的差别;(c)易于显示数据的变化趋势;(d)易于显示每组数据相对于总数的大小.统计图与特点选配方案分别是:①与(a);②与(c);③与(d);④与(b). 其中选配方案正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

