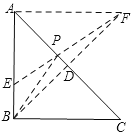
【题目】如图,E为等腰直角△ABC的边AB上的一点,要使AE=3,BE=1,P为AC上的动点,则PB+PE的最小值为____________.

参考答案:
【答案】5
【解析】试题分析:作点B关于AC的对称点F,构建直角三角形,根据最短路径可知:此时PB+PE的值最小,接下来要求出这个最小值,即求EF的长即可,因此要先求AF的长,证明△ADF≌△CDB,可以解决这个问题,从而得出EF=5,则PB+PE的最小值为5.
解:如图,过B作BD⊥AC,垂足为D,并截取DF=BD,连接EF交AC于P,连接PB、AF,则此时PB+PE的值最小,
∵△ABC是等腰直角三角形,
∴AB=CB,∠ABC=90°,AD=DC,
∴∠BAC=∠C=45°,
∵∠ADF=∠CDB,
∴△ADF≌△CDB,
∴AF=BC,∠FAD=∠C=45°,
∵AE=3,BE=1,
∴AB=BC=4,
∴AF=4,
∵∠BAF=∠BAC+∠FAD=45°+45°=90°,
∴由勾股定理得:EF=![]() =
=![]() =5,
=5,
∵AC是BF的垂直平分线,
∴BP=PF,
∴PB+PE=PF+PE=EF=5,
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中.有抛物线
 和
和 .抛物线
.抛物线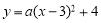 经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线
经过原点,与x轴正半轴交于点A,与其对称轴交于点B.P是抛物线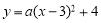 上一点,且在x轴上方.过点P作x轴的垂线交抛物线
上一点,且在x轴上方.过点P作x轴的垂线交抛物线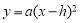 于点Q.过点Q作PQ的垂线交抛物线
于点Q.过点Q作PQ的垂线交抛物线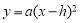 于点
于点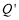 (不与点Q重合),连结
(不与点Q重合),连结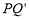 .设点P的横坐标为m.
.设点P的横坐标为m.(1)求a的值;
(2)当抛物线
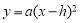 经过原点时,设△
经过原点时,设△ 与△OAB重叠部分图形的周长为l.
与△OAB重叠部分图形的周长为l.①求
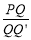 的值;
的值;②求l与m之间的函数关系式;
(3)当h为何值时,存在点P,使以点O、A、Q、
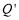 为顶点的四边形是轴对称图形?直接写出h的值.
为顶点的四边形是轴对称图形?直接写出h的值.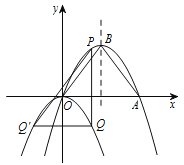
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°,点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动,当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFHG,设点E运动的时间为t秒
(1)求线段EF的长(用含t的代数式表示);
(2)求点H与点D重合时t的值;
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位,求S与t之间的函数关系式;
(4)矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,t的值为 ;当OO′⊥AD时,t的值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】若直角三角形的一个锐角为20°,则另一个锐角等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(x+y)﹣(x﹣y)的结果是
相关试题

