【题目】如图,在Rt△ABC中,CA=CB=2,M为CA的中点,在AB上存在一点P,连接PC、PM,则△PMC周长的最小值是( ) 
A.![]()
B.![]()
C.![]() +1
+1
D.![]() +1
+1
参考答案:
【答案】C
【解析】解:作点C关于直线AB的对称点D,连接DM交AB于点P,此时△PCM周长最小. 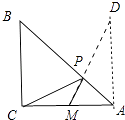
∵CA=CB,∠ACB=90°,
∴∠BAC=∠B=∠BAD=45°,
在RT△ADM中,∵∠DAM=90°,AD=2,AM=1,
∴DM= ![]() =
= ![]() ,
,
∴此时△PCM的周长为PC+PM+CM=PM+PD+CM= ![]() +1.
+1.
故选C.
【考点精析】利用轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果收入1000元记作+1000元,那么﹣800元表示( )
A. 支出200元 B. 收入200元
C. 支出800元 D. 收入800元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD//BC交y轴于点D.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD//BC交y轴于点D.(1)求平行线AD、BC之间的距离;
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
(3)如图2,将抛物线以每秒
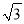 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作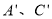 ,当
,当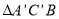 是以
是以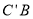 为底边的等腰三角形时,将等腰
为底边的等腰三角形时,将等腰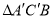 绕点D逆时针旋转一周,记旋转中的
绕点D逆时针旋转一周,记旋转中的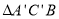 为
为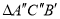 ,若直线
,若直线 与y轴交于点K,直线
与y轴交于点K,直线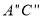 与直线AD交于点I,当
与直线AD交于点I,当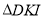 是以KI为底边的等腰三角形时,求出
是以KI为底边的等腰三角形时,求出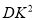 的值.
的值.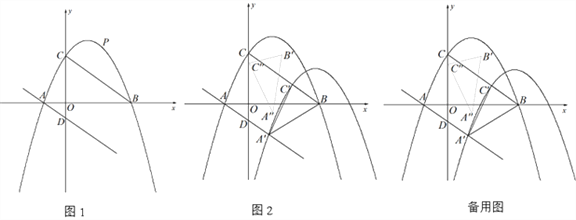
-
科目: 来源: 题型:
查看答案和解析>>【题目】x的平方的3倍与5的差,用代数式表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x=0的解为_____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣3xmy2与2x3yn是同类项,则m= , n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5cm,圆心O到直线的距离为6cm,则直线与⊙O的位置关系是_____.
相关试题

