Question

【题目】定义：数学活动课上，乐老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形．

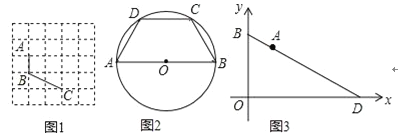
理解：（1）如图1，已知A、B、C在格点（小正方形的顶点）上，请在方格图中画出以格点为顶点，AB、BC为边的两个对等四边形ABCD；

（2）如图2，在圆内接四边形ABCD中，AB是⊙O的直径，AC=BD．求证：四边形ABCD是对等四边形；

（3）如图3，点D、B分别在x轴和y轴上，且D（8，0），B（0，6），点A在BD 边上，且AB=2．试在x轴上找一点C，使ABOC是对等四边形，请直接写出所有满足条件的C点坐标．

Answer 1

【答案】（1）四边形ABCD为对等四边形，图见解析；

（2）四边形ABCD是对等四边形；

（3）C点坐标为：（2，0）或（，0）．

【解析】

试题分析：（1）根据对等四边形的定义画出图形即可；

（2）根据圆周角定理得到∠ADB=90°，∠ACD=90°，根据直角三角形全等的判定定理证明Rt△ADB≌Rt△BCA，根据全等三角形的性质证明即可；

（3）分OC=AB、AC=OB两种情况，根据平行线分线段成比例定理计算即可．

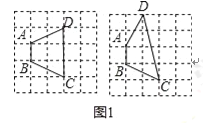
试题解析：（1）如图1：四边形ABCD为对等四边形；

（2）证明：∵AB是⊙O的直径，

∴∠ADB=90°，∠ACD=90°，

在Rt△ADB和Rt△BCA中，

，

∴Rt△ADB≌Rt△BCA，

∴AD=BC，

∴四边形ABCD是对等四边形；

（3）∵D（8，0），B（0，6），

∴OD=8，OB=6，∴BD=10，

∵AB=2，∴AD=8，

如图3，当OC=AB时，C点坐标为（2，0），

如图4，当AC=OB时，AC=6，

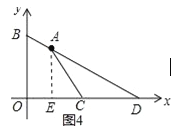
作AE⊥OD于E，

则AE∥OB，

∴，即，

解得，DE=，

∴，

OE=OD﹣DE=，

则OC=OE+EC=，

∴C点坐标为（，0），

∴四边形ABOC为对等四边形时，C点坐标为：（2，0）或（，0）．