【题目】如图,直线y=2x与双曲线y=![]() 在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为( )
在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为( )
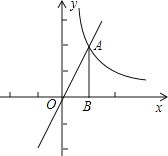
A.(1,0)
B.(1,0)或(﹣1,0)
C.(2,0)或(0,﹣2)
D.(﹣2,1)或(2,﹣1)
参考答案:
【答案】D
【解析】
试题分析:联立直线与反比例解析式,求出交点A的坐标,将△ABO绕点O旋转90°,得到△A′B′O,利用图形及A的坐标即可得到点A′的坐标.
解:联立直线与反比例解析式得:![]() ,
,
消去y得到:x2=1,
解得:x=1或﹣1,
∴y=2或﹣2,
∴A(1,2),即AB=2,OB=1,
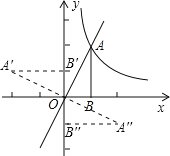
根据题意画出相应的图形,如图所示,
可得A′B′=A′′B′′=AB=2,OB′=OB′′=OB=1,
根据图形得:点A′的坐标为(﹣2,1)或(2,﹣1).
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前我省小学和初中在校生共136万人,其中小学在校生人数比初中在校生人数的2倍少2万人.问目前我省小学和初中在校生各有多少万人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y=
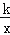 的图象交于点A(﹣1,n).
的图象交于点A(﹣1,n).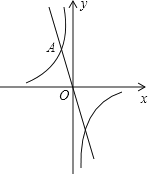
(1)求反比例函数y=
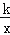 的解析式;
的解析式;(2)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y1=x2+2x+m﹣5.
(1)如果该二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如果该二次函数的图象与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(1,0),求它的表达式和点C的坐标;
(3)如果一次函数y2=px+q的图象经过点A、C,请根据图象直接写出y2<y1时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列轴对称图形中,对称轴条数最多的是 ( )
A. 线段 B. 等边三角形 C. 正方形 D. 圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中计算正确的是( )
A. (-a2)5 =-a10 B. (x4)3= x7 C. b5·b5= b25 D. a6÷a2=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.

相关试题

