【题目】如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角的两边分别交AB、AC边于M、N两点,连接MN.


探究:在下面两种条件下,线段BM、MN、NC之间的关系,并加以证明.
①AN=NC(如图②); ②DM//AC(如图③).
思考:若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图④中画出图形,并说明理由.
参考答案:
【答案】(1)MN=NC+BM,证明见解析
(2)MN=NC-BM,证明见解析
【解析】
本题是一个典型的“半角旋转”模型。①和②情况其实是一样的,延长AC至E,使得CE=BM并连接DE,构造全等三角形,找到MD=DE,∠BDM=∠CDE,BM=CE,再进一步证明△DMN≌△DEN,进而得到MN=BM+NC;
思考题:MN=NC-BM.仿(1)的思路运用截长法证明.
(1)MN=BM+NC.理由如下:
延长AC至E,使得CE=BM,连接DE,如图所示:
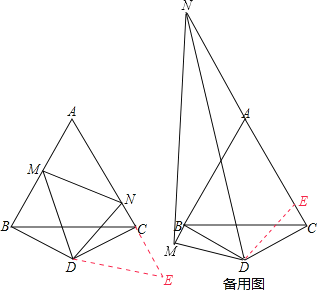
∵△BDC为等腰三角形,△ABC为等边三角形,
∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,
又BD=DC,且∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,
∴∠MBD=∠ECD=90°.
∴△MBD≌△ECD(SAS),
∴MD=DE,∠BDM=∠CDE,BM=CE,
又∵∠BDC=120°,∠MDN=60°,
∴∠BDM+∠NDC=∠BDC-∠MDN=60°,
∴∠CDE+∠NDC=60°,即∠NDE=60°,
∵∠MDN=∠NDE=60°.
∴△DMN≌△DEN(SAS),
∴MN=EN.
又NE=NC+CE,BM=CE,
∴MN=BM+NC;
(2)MN=NC-BM.
证明:在CA上截取CE=BM.
由(1)知:∠DCE=∠DBM=90°,DC=DB.
又CE=BM,
∴△DCE≌△DBM (SAS)
∴∠CDE=∠BDM,DM=DE.
∴∠MDN=∠EDN=60°.
∴△MDN≌△EDN (SAS)
∴NM=NE.
∵NE=NC-CE,CE=BM,
∴MN=NC-BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从正五边形的五个顶点中,任取四个顶点连成四边形,对于事件M:“这个四边形是等腰梯形” .下列判断正确的是( )
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为
 D. 事件M发生的概率为
D. 事件M发生的概率为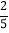
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
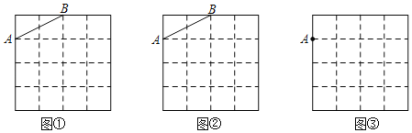
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形ABC;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形,这个正方形的面积= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
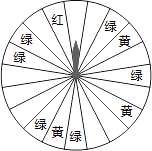
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个黑球的概率是
 ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
相关试题

