Question

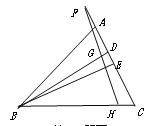
【题目】如图，△ABC中，BD、BE分别是高和角平分线，点F在CA的延长线上，FH⊥BE，交BD于点G，交BC于点H；下列结论：①∠DBE=∠F；②2∠BEF=∠BAF+∠C；③∠F=∠BAC-∠C；④∠BGH=∠ABE+∠C，其中正确的结论有___________．

Answer 1

【答案】①②③④

【解析】①∵BD⊥FD，

∴∠FGD+∠F=90°，

∵FH⊥BE，

∴∠BGH+∠DBE=90°，

∵∠FGD=∠BGH，

∴∠DBE=∠F，

①正确；

②∵BE平分∠ABC，

∴∠ABE=∠CBE，

∠BEF=∠CBE+∠C，

∴2∠BEF=∠ABC+2∠C，

∠BAF=∠ABC+∠C，

∴2∠BEF=∠BAF+∠C，

②正确；

③∠ABD=90°-∠BAC，

∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC，

∵∠CBE=90°-∠C，

∴∠DBE=∠BAC-∠C，

由①得，∠DBE=∠F，

∴∠F=∠BAC-∠C，

③正确；

④∵∠AEB=∠EBC+∠C，

∵∠ABE=∠CBE，

∴∠AEB=∠ABE+∠C，

∵BD⊥FC，FH⊥BE，

∴∠BGH=∠ABE，

∴∠BGH=∠ABE+∠C，

④正确，

故答案为：①②③④．