【题目】(1)问题发现:如图1,![]() 是等边三角形,点
是等边三角形,点![]() 是边
是边![]() 上的一点,过点
上的一点,过点![]() 作
作![]() 交
交![]() 于
于![]() ,则线段
,则线段![]() 与
与![]() 有何数量关系是______;
有何数量关系是______;


(2)拓展探究:如图2,将![]() 绕点
绕点![]() 逆时针旋转角
逆时针旋转角![]() ,上面的结论是否仍然成立?如果成立,请就图2给出的情况加以证明;
,上面的结论是否仍然成立?如果成立,请就图2给出的情况加以证明;

(3)问题解决:如果![]() 的边长为4,
的边长为4,![]() ,直接写出当
,直接写出当![]() 旋转
旋转![]() 、
、![]() 、
、![]() 在同一条直线上时
在同一条直线上时![]() 的长.
的长.
参考答案:
【答案】(1)![]() ,见解析;(2)仍然成立,见解析;(3)
,见解析;(2)仍然成立,见解析;(3)![]() 或
或![]() .
.
【解析】
(1)根据等边三角形的性质得到∠B=∠C=60°,AB=AC,再利用平行的性质证得∠ADE=∠AED,从而得到AD=AE,最后根据线段之间的关系即可得到结论;
(2)证明△BAD≌△CAE,即可得到结论;
(3)分顺时针旋转和逆时针旋转两种情况,画出图形,然后根据线段之间的关系即可计算出BE的长度.
解:(1)BD=CE,理由是:
∵△ABC是等边三角形,
∴AB=AC,∠B=∠C=60°,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠ADE=∠AED=60°,
∴AD=AE,
∴AB-AD=AC-AE,
∴BD=CE;
(2)仍然成立.
证明:∵![]() 是等边三角形,DE∥BC,
是等边三角形,DE∥BC,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)当![]() 顺时针旋转到
顺时针旋转到![]() 、
、![]() 、
、![]() 在同一条直线上时:
在同一条直线上时:

∴BE=AB-AE=4-2=2,
当![]() 逆时针旋转到
逆时针旋转到![]() 、
、![]() 、
、![]() 在同一条直线上时:
在同一条直线上时:
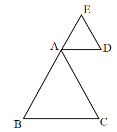
∴BE=AB+AE=4+2=6,
综上所述,BE=2或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为
为 所在平面内一点,且
所在平面内一点,且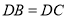 ,
, ,
, ,垂足分别为点
,垂足分别为点 、
、 ,
, .
.(1)如图1,当点
 在
在 边上时,判断
边上时,判断 的形状;并证明你的结论;
的形状;并证明你的结论;
(2)如图2,当点
 在
在 内部时,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请举出反例(画图说明,不需证明).
内部时,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请举出反例(画图说明,不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则
 的值等于_____.
的值等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出
 关于
关于 轴对称的
轴对称的 .
.(2)写出点
 的坐标(直接写答案).
的坐标(直接写答案).A1_____________,B1______________,C1______________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC于D,AD=BD,AC=BE.
(1)求证:∠BED=∠C;
(2)猜想并说明BE和AC有什么数量和位置关系。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,ACB和DCE都是等腰直角三角形,∠ACB=∠DCE=90
 ,连接AE、BD交于点O. AE与DC交于点M,BD与AC交于点N.
,连接AE、BD交于点O. AE与DC交于点M,BD与AC交于点N.(1)如图①,求证:AE=BD;
(2)如图②,若AC=DC,在不添加任何辅助线的情况下,请直接写出图②中四对全等的直角三角形.

相关试题

