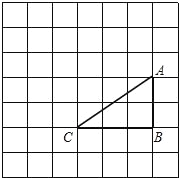
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
参考答案:
【答案】(1)图见解析,A1的坐标为(﹣1,4),点B1的坐标为(1,4);(2)![]() +3.
+3.
【解析】
试题分析:(1)根据旋转中心方向及角度找出点A、B的对应点A1、B1的位置,然后顺次连接即可,根据A、B的坐标建立坐标系,据此写出点A1、B1的坐标;(2)利用勾股定理求出AC的长,根据△ABC扫过的面积等于扇形CAA1的面积与△ABC的面积和,然后列式进行计算即可.
试题解析:(1)所求作△A1B1C如图所示:
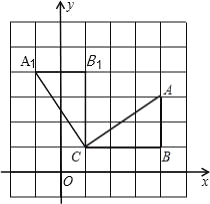
由A(4,3)、B(4,1)可建立如图所示坐标系,
则点A1的坐标为(﹣1,4),点B1的坐标为(1,4);
(2)∵AC=![]() ,∠ACA1=90°
,∠ACA1=90°
∴在旋转过程中,△ABC所扫过的面积为:
S扇形CAA1+S△ABC
=![]() +
+![]() ×3×2
×3×2
=![]() +3.
+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对话,解答问题:

(1)分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a,b)的所有取值;
(2)求在(a,b)中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y=
 x2﹣
x2﹣ x+3的绳子.
x+3的绳子.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为
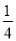 ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示.

(1)①c+b0 ②a+c0 ③b﹣a0(填“>”“<”或“=”)
(2)试化简:|b﹣a|+|a+c|﹣|c+b| -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2+2ab+b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】样本数据3,5,n,6,8的众数是8,则这组数的中位数是( )
A.3B.5C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)10+(﹣20)﹣(﹣8)
(2)(﹣2)÷ ×(﹣3)
×(﹣3)
(3)20﹣(﹣5)2×(﹣2)
(4)﹣14﹣|﹣5|+(﹣3)3÷(﹣22)
(5) ×(﹣
×(﹣  )÷
)÷  ×(﹣
×(﹣  +
+  +
+  )×72﹣(﹣2)2÷4﹣1.
)×72﹣(﹣2)2÷4﹣1.
相关试题

