【题目】如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).

(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使![]() 与
与![]() 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①点P(1,6)或(3,2);②存在,点P的坐标为(2,4)或点P(
;(2)①点P(1,6)或(3,2);②存在,点P的坐标为(2,4)或点P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)由于A(4,0).B(0,8),利用待定系数法即可求出直线AB的解析式;
(2)①可以设动点P(x,﹣2x+8),由此得到PE=x,PF=﹣2x+8,再利用矩形OEPF的面积为6即可求出点P的坐标;
②存在,分两种情况:第一种由CP∥OB得△ACP∽△AOB,由此即可求出P的坐标;第二种CP⊥AB,根据已知条件可以证明APC∽△AOB,
然后利用相似三角形的对应边成比例即可求出PA,再过点P作PH⊥x轴,垂足为H,由此得到PH∥OB,进一步得到△APH∽△ABO,然后利用相似三角形的对应边成比例就可以求出点P的坐标.
试题解析:(1)设直线AB的解析式为![]() ,依题意
,依题意
![]() ,解得:
,解得:![]()
∴![]() ;
;
(2)①设动点P (x,![]() )
)
则![]() ,
,![]()
∴![]()
∴![]() ,
,![]()
经检验![]() ,
,![]() 都符合题意
都符合题意
∴点P(1,6)或(3,2);
②存在,分两种情况
第一种:![]()
∴![]() ∽
∽![]()

而点C的坐标为(2,0)
∴点P(2,4 )
第二种![]()
∵![]() ,
,![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∴![]()
如图,过点P作![]() 轴,垂足为H
轴,垂足为H

∴![]()
∴![]() ∽
∽![]()
∴![]()
∴
∴![]() ,
,![]()
∴![]()
∴点P(![]() ,
,![]() )
)
∴点P的坐标为(2,4)或点P(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC∽△DEF , 若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上中线的比为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中结果为负数的是( )
A. ﹣(﹣3) B. |﹣3| C. (﹣3)2 D. ﹣32
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△OAB中, CD∥AB,若OC:OA =1:2,则下列结论:(1)
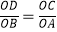 ;(2);(3)
;(2);(3)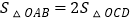 . 其中正确的结论是( )
. 其中正确的结论是( )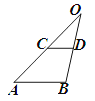
A.(1)(2)
B.(1)(3)
C.(2)(3)
D.(1)(2)(3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AA1∥BB1∥CC1 , 如果
 , AA1=2,CC1=6,那么线段BB1的长是 .
, AA1=2,CC1=6,那么线段BB1的长是 .
-
科目: 来源: 题型:
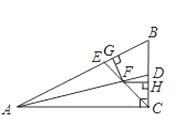
查看答案和解析>>【题目】如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,且FG⊥AB于G,FH⊥BC于H.
(1)求证:∠BEC=∠ADC;
(2)请你判断并FE与FD之间的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(﹣1,1)位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

