【题目】如图,已知点(1,3)在函数y=![]() 的图象上,矩形ABCD的边BC在x轴正半轴上,E是对角线BD的中点,函数y=
的图象上,矩形ABCD的边BC在x轴正半轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
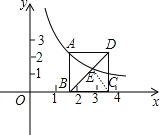
(1)求k的值;
(2)求点C的横坐标(用m表示);
(3)当∠ABD=45°,求m的值.
参考答案:
【答案】(1)k=3;(2)点C(![]() m,0).(3)m=
m,0).(3)m=![]() .
.
【解析】
试题分析:(1)把(1,3)代入反比例函数解析式即可;
(2)BG=CG,求出OB即可,A在反比例函数解析式上,求出AB,即A的纵坐标,代入求出A的横坐标,求出BG和CG,求出OC,即可求出答案;
(3)∠ABD=45°时,AB=BD,把(2)中的代数式代入即可求解.
解:(1)∵点(1,3)在函数y=![]() 的图象上,
的图象上,
∴3=![]() ,即k=3;
,即k=3;
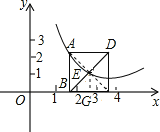
(2)连接AC,则AC过E,过E做EG⊥BC交BC于G点,
∵点E的横坐标为m,E在双曲线y=![]() 上,
上,
∴E的纵坐标是y=![]() ,
,
∵E为BD中点,
∴由平行四边形性质得出E为AC中点,
∴BG=GC=![]() BC,
BC,
∴AB=2EG=![]() ,
,
即A点的纵坐标是![]() ,
,
代入双曲线y=![]() 得:A的横坐标是
得:A的横坐标是![]() m,
m,
∴OB=![]() m,
m,
即BG=GC=m﹣![]() m=
m=![]() m,
m,
∴CO=![]() m+m=
m+m=![]() m,
m,
∴点C(![]() m,0).
m,0).
(3)当∠ABD=45°时,AB=AD,则有![]() =m,即m2=6,
=m,即m2=6,
解之m1=![]() ,m2=﹣
,m2=﹣![]() (舍去),
(舍去),
∴m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3﹣a2=a B. a2a3=a6 C. (2a)2=4a2 D. a6÷a3=a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】-27的立方根是( )
A. -3 B. 3 C. ±3 D. 不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】“线段、角、等腰三角形、直角三角形”中一定是轴对称图形有____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.
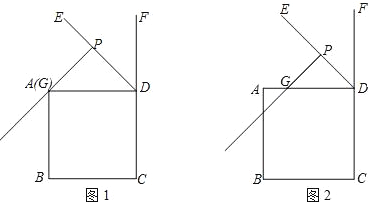
(1)如图1,若点G与点A重合.
①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
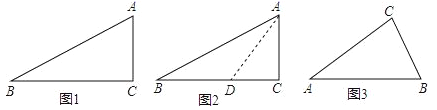
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°= .
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣3x2﹣1向右平移1个单位长度,再向上平移1个单位长度后所得的抛物线的解析式为( )
A.y=﹣3(x﹣1)2
B.y=﹣3(x+1)2
C.y=﹣3(x﹣1)2+2
D.y=﹣3(x﹣1)2﹣2
相关试题

