【题目】如图,在等腰△ABC中,CB=CA,延长AB至点D,使DB=CB,连接CD,以CD为边作等腰△CDE,使CE=CD,∠ECD=∠BCA,连接BE交CD于点M.

(1)BE=AD吗?请说明理由;
(2)若∠ACB=40°,求∠DBE的度数.
参考答案:
【答案】(1)BE=AD;理由见解析;(2)∠DBE =40°.
【解析】(1)求出∠BCE=∠ACD,根据SAS证出△BCE≌△ACD,得出对应边相等即可;
(2)由等腰三角形的性质和三角形内角和定理求出∠A=∠ABC=70°,由△BCE≌△ACD,得出对应角相等∠EBC=∠A=70°,再由三角形的外角性质得出∠DBE=∠ACB=40°即可.
解:(1)BE=AD;理由如下:
∵∠ECD=∠BCA,∴∠ECD+∠BCD=∠BCA+∠BCD,∴∠BCE=∠ACD,
在△BCE和△ACD中, ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD.
(2)∵CB=CA,∠ACB=40°,∴∠A=∠ABC=70°,
由(1)得:△BCE≌△ACD,∴∠EBC=∠A=70°,
∵∠DBC=∠DBE+∠EBC=∠ACB+∠ACB,
∴∠DBE=∠ACB=40°.
“点睛”本题考查了全等三角形的判定与性质、等腰三角形的性质、三角形内角和定理、三角形外角和性质;证明三角形全等是解决其他的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表: 频数分布表
身高分组
频数
百分比
x<155
5
10%
155≤x<160
a
20%
160≤x<165
15
30%
165≤x<170
14
b
x≥170
6
12%
总计
100%
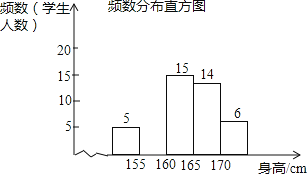
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD上底的长是4,下底的长是x,高是6.

(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价25%后的售价为1.25元,则该商品在甲商场的原价为 元;
(2)乙商场定价有两种方案:方案将该商品提价20%;方案将该商品提价1元。某顾客发现在乙商场用60元钱购买该商品,按方案购买的件数是按方案购买的件数的2倍少10件,求该商品在乙商场的原价是多少?
(3)甲、乙两商场把该商品均按原价进行了两次价格调整.甲商场:第一次提价的百分率是a,第二次提价的百分率是b;乙商场:两次提价的百分率都是
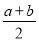 (a>0,b>0,a≠b).请问甲、乙两商场,哪个商场的提价较多?请说明理由.
(a>0,b>0,a≠b).请问甲、乙两商场,哪个商场的提价较多?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】第二象限内的点P(x,y)满足|x|=9,y2=4,则点P的坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABC 的内角分别为A 、B 、C ,下列能判定ABC 是直角三角形的条件是( )
A.A 2B 3CB.C 2BC.A : B : C 3 : 4 : 5D.A B C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果等腰三角形有一条边长是6,另一条边长是8,那么它的周长是( )
A.20
B.20或22
C.22
D.24
相关试题

