【题目】甲、乙两站相距300千米,一列慢车从甲站开往乙站,每小时行40千米,一列快车从乙站开往甲站,每小时行80千米,已知慢车先行1.5小时,快车再开出,则快车开出多少小时后与慢车相遇?
参考答案:
【答案】快车开出2小时后与慢车相遇.
【解析】试题分析:设快车开出xh后与慢车相遇,等量关系为:慢车走的路程+快车走的路程=300km,据此列方程求解.
试题解析:设快车开出x小时后与慢车相遇,则此时慢车开出(x+1.5)小时,
根据题意得:80x+40(x+1.5)=300,
解得:x=2.
答:快车开出2小时后与慢车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.平行四边形的对角线互相平分且相等B.矩形的对角线相等且互相平分
C.菱形的对角线互相垂直且相等D.正方形的对称轴是正方形的对角线
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=a(x-h)2+k(a≠0)的顶点坐标是______,对称轴是______,当x=______时,y有最值______;当a>0时,若x______时,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策,某中学为了提高学生参与“五水共治”的积极性举行了“五水共治”知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
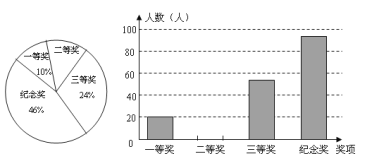
(1)这次知识竞赛共有多少名学生?
(2)浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策, “二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2的顶点,坐标为______,对称轴是______.当x______时,y随x增大而减小;当x______时,y随x增大而增大;当x=______时,y有最______值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形内角和为900°,则这个多边形是____边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ABCD中,∠A+∠C=240°,则∠B的度数是
相关试题

