Question

【题目】如图1，在平面直角坐标系中，点A、点B的坐标分别为（4，0）、（0，3）.

(1)求AB的长度.

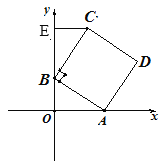
(2)如图2，若以AB为边在第一象限内作正方形ABCD,求点C的坐标.

(3)在x轴上是否存一点P，使得⊿ABP是等腰三角形？若存在，直接写出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】(1) 5 (2) (3，7)（3）（-1，0）、（-4，0）、（9，0）、（，0）

【解析】试题分析: (1)根据勾股定理即可求出;

(2)过点C向y轴作垂线,通过证明三角形全等就能求出点C的坐标;

(3)分三种情况: ①AB=BP; ②AB=AP; ③PA=PB,分别求出即可.

试题解析:

(1) ∵点A、点B的坐标分别为（4，0）、（0，3）,

∴OA=4,OB=3,

∴AB==5.

(2) 过点C作CE⊥y轴,

∵∠BOA＝90°，

∴∠OBA＋∠BAO＝90°．

又∵∠CBA=90°，

∴∠CBE＋∠ABO＝90°，

∴∠CBE＝∠BAO．

在△ABO和△CAD中，

，

∴△ABO≌△BCE（AAS）；

∴CE＝OB＝3，BE＝OA＝4，OE＝OA＋AD＝7．

∴C的坐标是（3，7）；

（3）存在．

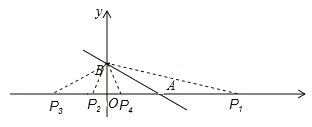
①若AP＝AB，则P（9，0），P（-1，0）；

②若AB＝BP，则OP＝OA＝4，∴P（4，0）；

③若AP＝BP，

设OP＝m，则AP＝BP＝OAOP＝4m，

∵OB＋OP＝BP，

∴3＋m＝（4m），

解得：m＝，

∴；

综上可得：点P的坐标为：（-1，0）、（-4，0）、（9，0）、.