【题目】在△ABC中,AB=13 cm,AC=20 cm,BC 边上的高为12 cm,求△ABC 的面积.
参考答案:
【答案】126 cm2或66 cm2
【解析】试题分析:
分两种情况:①∠B为锐角;②∠B为钝角;利用勾股定理求出BD、CD,即可求出BC的长.
试题解析:
当∠B 为锐角时(图①),
在Rt△ABD中,
BD=![]() =5(cm).
=5(cm).
在Rt△ADC中,
CD=![]() =16(cm).
=16(cm).
∴BC=BD+CD=5+16=21(cm).
∴S△ABC=![]() BC·AD=
BC·AD=![]() ×21×12=126(cm2).
×21×12=126(cm2).
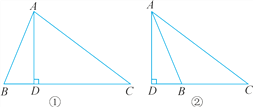
当∠B 为钝角时(图②),
同理,BC=CD-BD=16-5=11(cm).
∴S△ABC=![]() BC·AD=
BC·AD=![]() ×11×12=66(cm2).
×11×12=66(cm2).
∴△ABC 的面积为126 cm2或66 cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把某不等式组中两个不等式的解集表示在数轴上,如图所示,则这个不等式组可能是 ( )
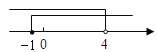
A.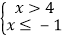
B.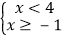
C.
D.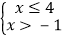
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点M,N分别在边OA,OB上,且OM=1,ON=3,点P,Q分别在边OB,OA上,求MP+PQ+QN的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a+1,﹣
 +1)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
+1)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.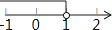
B.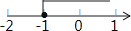
C.
D.
-
科目: 来源: 题型:
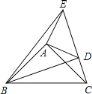
查看答案和解析>>【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2).
错误的结论有 (填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地上午的气温为零上3℃,记作3℃,那么这天傍晚为零下6℃,记作℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|m﹣2|+(n+3)2=0,则m﹣n= .
相关试题

