【题目】(1)如图1,若CO⊥AB,垂足为O,OE、OF分别平分∠AOC与∠BOC.求∠EOF的度数;
(2)如图2,若∠AOC=∠BOD=80°,OE、OF分别平分∠AOD与∠BOC.求∠EOF的度数;
(3)若∠AOC=∠BOD=α,将∠BOD绕点O旋转,使得射线OC与射线OD的夹角为β,OE、OF分别平分∠AOD与∠BOC.若α+β≤180°,α>β,则∠EOC= .(用含α与β的代数式表示)

参考答案:
【答案】(1)90°;(2)80°;(3)![]()
【解析】
试题分析:(1)根据垂直的定义得到∠AOC=∠BOC=90°,根据角平分线的定义即可得到结论;
(2)根据角平分线的定义得到∠EOD=![]() ∠AOD=
∠AOD=![]() ×(80+β)=40+
×(80+β)=40+![]() β,∠COF=
β,∠COF=![]() ∠BOC=
∠BOC=![]() ×(80+β)=40+
×(80+β)=40+![]() β,根据角的和差即可得到结论;
β,根据角的和差即可得到结论;
(3)如图2由已知条件得到∠AOD=α+β,根据角平分线的定义得到∠DOE=![]() (α+β),即可得到结论.
(α+β),即可得到结论.
解:(1)∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∵OE平分∠AOC,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() ×90°=45°,
×90°=45°,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=
∠BOC=![]() ×90°=45°,
×90°=45°,
∠EOF=∠EOC+∠COF=45°+45°=90°;
(2)∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() ×(80+β)=40+
×(80+β)=40+![]() β,
β,
∵OF平分∠BOC,
∴∠COF=![]() ∠BOC=
∠BOC=![]() ×(80+β)=40+
×(80+β)=40+![]() β,
β,
∠COE=∠EOD﹣∠COD=40+![]() β﹣β=40﹣
β﹣β=40﹣![]() β;
β;
∠EOF=∠COE+∠COF=40﹣![]() β+40+
β+40+![]() β=80°;
β=80°;
(3)如图2,∵∠AOC=∠BOD=α,∠COD=β,

∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE=![]() (α+β),
(α+β),
∴∠COE=∠DOE﹣∠COD=![]() =
=![]() ,
,
如图3,∵∠AOC=∠BOD=α,∠COD=β,
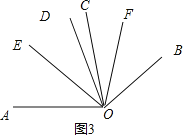
∴∠AOD=α+β,
∵OE平分∠AOD,
∴∠DOE=![]() (α﹣β),
(α﹣β),
∴∠COE=∠DOE+∠COD=![]() .
.
综上所述:![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A向左移动2个单位长度到达点 A1,第二次将点A1,向右移动4个单位长度到达点A2,第三次将点A2向左移动6个单位长度到达点A3,按照这种移动规律移动下去,第n次移动到点An,如果点An与原点的距离等于19,那么n的值是__.
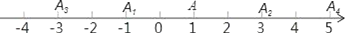
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,那么圆弧形桥拱所在圆的半径是米.
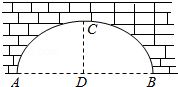
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n=_.
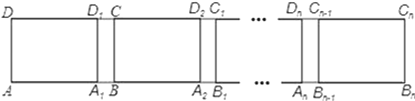
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
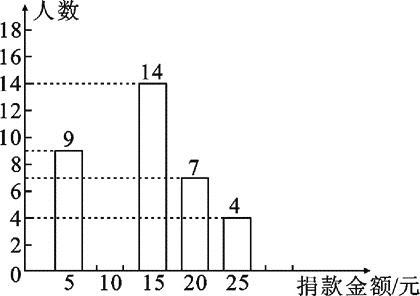
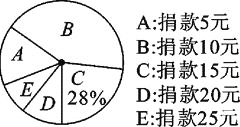
(1)本次共抽查学生________人,并将条形图补充完整;
(2)捐款金额的众数是________,平均数是________,中位数为________.
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?
相关试题

