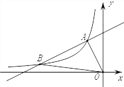
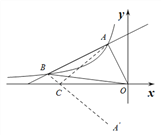
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)P点坐标为(
;(3)P点坐标为(![]() ,0)
,0)
【解析】分析:(1)由点A的坐标求反比例函数的解析式,得到点B的坐标,待定系数法求一次函数的解析式;(2)分别过点A,B用坐标轴的平行线构造矩形,用图形面积的和差关系求三角形AOB的面积;(3)作点A关于x轴的对称点A′,直线A′B与x轴的交点即是点P.
详解:(1)∵反比例![]() 的图象经过点A(—1,2),
的图象经过点A(—1,2),
∴![]() =—1×2=—2,
=—1×2=—2,
∴反比例函数表达式为:![]() ,
,
∵反比例![]() 的图象经过点B(—4,n),
的图象经过点B(—4,n),
∴—4n=—2,![]() ,∴B点坐标为(—4,
,∴B点坐标为(—4,![]() ),
),
∵直线![]() 经过点A(—1,2),点B(—4,
经过点A(—1,2),点B(—4,![]() ),
),
∴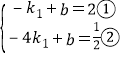 ,
,
①—②,得:3![]() ,∴
,∴![]() ,
,
把![]() 代入①,得:b=
代入①,得:b=![]() ,
,
∴一次函数表达式为:![]() .
.
(2)如图1所示,分别过点B作BD⊥x轴,垂足为D,过点A作AE⊥y轴,垂足为E,则四边形ODFE为矩形,
∵点A(—1,2),点B(—4,![]() ),
),
∴OD=EF=4,OE=DF=2,AE=1,BD=![]() ,
,
∴![]() ,
,![]() .
.
∵点A,点B在函数![]() 的图象上,∴
的图象上,∴![]()
∴![]() .
.
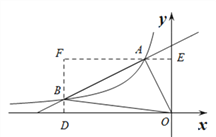
(3)如图2所示,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,
∵点A′和A(—1,2)关于x轴对称,∴点A′的坐标为(—1,—2),
设直线A′B的表达式为![]()
∵经过点A′(—1,—2),点B(—4,![]() ),∴
),∴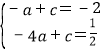
解得:![]() ,
,![]() .
.
∴直线A′B的表达式为:![]() .
.
当y=0时,则x=![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0).
,0).
-
科目: 来源: 题型:
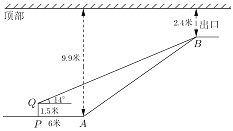
查看答案和解析>>【题目】地铁10号线某站点出口横截面平面图如图所示,电梯
 的两端分别距顶部9.9米和2.4米,在距电梯起点
的两端分别距顶部9.9米和2.4米,在距电梯起点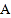 端6米的
端6米的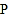 处,用1.5米的测角仪测得电梯终端
处,用1.5米的测角仪测得电梯终端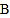 处的仰角为14°,求电梯
处的仰角为14°,求电梯 的坡度与长度.(参考数据:
的坡度与长度.(参考数据: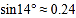 ,
,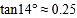 ,
,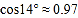 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的一条弦,点O在线段AC上,AC=AB,OC=3,sinA=
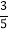 .求:(1)圆O的半径长;(2)BC的长.
.求:(1)圆O的半径长;(2)BC的长.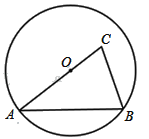
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是数值转换机的示意图,图②是小亮按照其对应关系画出的y与x的函数图象.已知点A的坐标为(0,3),点B的横坐标为4.
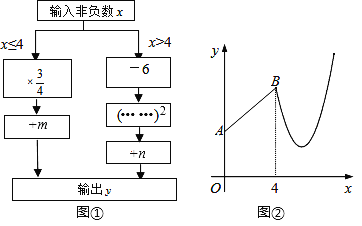
(1)求m、n的值.
(2)求输出y的最小值.
(3)当y=4时,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机普及率的提高,有些人开始过分依赖手机,一天中使用手机时间过长而形成了“手机瘾”,某校学生会为了了解本校初三年级的手机使用情况,随机调查了部分学生的手机使用时间,将调查结果分成五类:
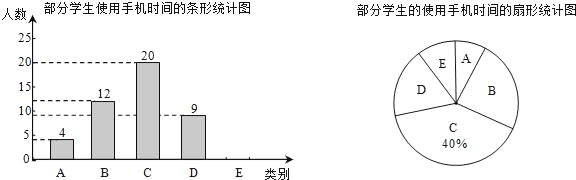
A、基本不用;B、平均每天使用1~2h;C、平均每天使用2~4h;D、平均每天使用4~6h;E、平均每天使用超过6h,并根据统计结果绘制成了如下两幅不完整的统计图.
(1)学生会一共调查了多少名学生?
(2)此次调查的学生中属于E类的学生有 人,并补全条形统计图;
(3)若一天中手机使用时间超过6h,则患有严重的“手机瘾”,该校初三学生共有900人,请估计该校初三年级中患有严重的“手机瘾”的人数.
-
科目: 来源: 题型:
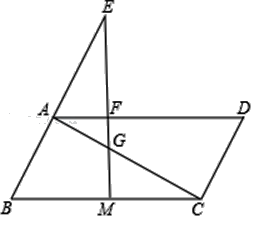
查看答案和解析>>【题目】已知,如图,在平行四边形ABCD中,M是BC边的中点,E是边BA延长线上的一点,连结EM,分别交线段AD、AC于点F、G.
(1)求证:
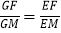 ;
;(2)当BC2=2BABE时,求证:∠EMB=∠ACD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=
 +bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.(1)直接写出抛物线的解析式为 ;
(2)以点E为圆心的⊙E与直线AB相切,求⊙E的半径;
(3)连接BC,点P是第三象限内抛物线上的动点,连接PE交线段BC于点D,当△CED为直角三角形时,求点P的坐标.

相关试题

