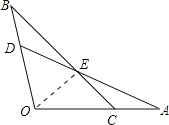
【题目】如图,OA=OB,∠A=∠B,有下列4个结论:①△AOD≌△BOC,②EA=EB,③点E在∠O的平分线上.④若OC=2CA,△AEC的面积为1,那么四边形OCED的面积为4.其中正确的结论个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】
根据全等三角形的判定得出△AOD≌△BOC(ASA),则OD=CO,从而证出△ACE≌△BDE,连接OE,可证明△AOE≌△BOE,则得出点E在∠O的平分线上,根据△AOE≌△BOE、△ACE≌△BDE即可求得S△ACE=S△OCE=S△ODE=S△BDE=1,即可解题.
①在△AOD和△BOC中,
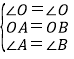 ,
,
∴△AOD≌△BOC(ASA),故①正确;
∴OD=CO,
∴BD=AC,
②在△ACE和△BDE中,
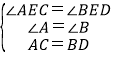 ,
,
∴△ACE≌△BDE(AAS),
∴AE=BE,故②正确;
③连接OE,
在△AOE和△BOE中,
 ,
,
∴△AOE≌△BOE(SSS),
∴∠AOE=∠BOE,
∴点E在∠O的平分线上,故③正确;
④∵OC=2CA,
∴OD=2BD,
∴S△ACE=S△BDE=1,
∵△AOE≌△BOE,△ACE≌△BDE,
∴S△ODE=2S△BDE=2,
∴四边形OCED的面积为4,故④正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为
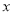 吨,应交水费为
吨,应交水费为 元,写出
元,写出 与
与 之间的函数关系式;
之间的函数关系式;(3)小黄家3月份用水26吨,他家应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为
 ,求EF的长.
,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7)且与直线y=kx﹣2k﹣3相交于点P(m,2m﹣7).

(1)求抛物线的解析式;
(2)求直线y=kx﹣2k﹣3与抛物线y=ax2﹣(2a+1)x+b的对称轴的交点Q的坐标;
(3)在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒前进或后退1步,并且每步的距离为一个单位长度,
 表示第n秒时机器人在数轴上位置所对应的数。则下列结论中正确的有______.(只需填入正确的序号)
表示第n秒时机器人在数轴上位置所对应的数。则下列结论中正确的有______.(只需填入正确的序号)①
 ②
② ③
③ ④
④
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.

(1).请用两种不同的方法表示图中阴影部分的面积.
方法①: ;
方法②: .
(2).由 (1)可得出
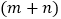 2,
2, ,4mn这三个代数式之间的一个等量关系为: .
,4mn这三个代数式之间的一个等量关系为: .(3)利用(2)中得到的公式解决问题:已知2a+b=6,ab=4,试求
 的值.
的值.
相关试题

