【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切 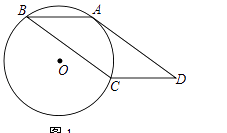
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E= ![]() ,求tan∠D
,求tan∠D 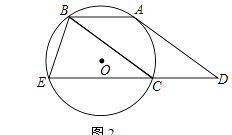
参考答案:
【答案】
(1)证明:证明:连接OA交BC于F.
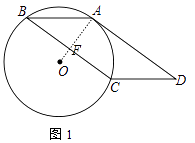
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分 ![]() ,
,
即 ![]() =
= ![]() .
.
(2)解:如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.
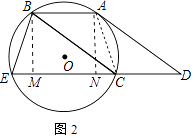
∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BE=AB=AC, ![]() =
= ![]() ,
,
∴∠E=∠ACE,
在Rt△BEM中,sin∠E= ![]() ,设BE=13m,则BM=12m,EM=5m,
,设BE=13m,则BM=12m,EM=5m,
在Rt△ANC中,sin∠ACN=sin∠E= ![]() ,AC=EB=13m,则CN=5m,
,AC=EB=13m,则CN=5m,
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠D= ![]() .
.
【解析】(1.)如图1中,连接OA交BC于F.只要证明OF⊥BC即可解决问题. (2.)如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.首先证明BE=AB=AC, ![]() =
= ![]() ,推出∠E=∠ACE,在Rt△BEM中,sin∠E=
,推出∠E=∠ACE,在Rt△BEM中,sin∠E= ![]() ,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E=
,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E= ![]() ,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE=
,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE= ![]() =
= ![]() =
= ![]() ,可得tan∠D=
,可得tan∠D= ![]() .
.
【考点精析】掌握平行四边形的性质和切线的性质定理是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
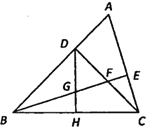
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形ABC中,若AB=16cm,AC=12cm,BC=20cm.点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,如果点P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,请用含t的代数式表示,①当点Q在AC上时,CQ= ;②当点Q在AB上时,AQ= ;
③当点P在AB上时,BP= ;④当点P在BC上时,BP= .
(2)如图2,若点P在线段AB上运动,点Q在线段CA上运动,当QA=AP时,试求出t的值.
(3)如图3,当P点到达C点时,P、Q两点都停止运动,当AQ=BP时,试求出t的值.
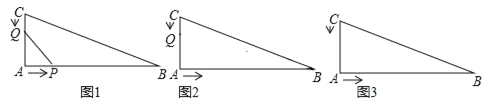
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的三分线,在△ABC中,∠B=30°,AD和 DE是△ABC的三分线,点D在 BC 边上,点E在 AC边上,且AD=BD,DE=CE,请写出∠C所有可能的度数________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面积
(2) 在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标
(3) 是否存在一点P到AC、AB的距离相等,同时到点A、点B的距离也相等.若存在保留作图痕迹标出点P的位置,并简要说明理由;若不存在,请说明理由
相关试题

