【题目】如图,抛物线 ![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.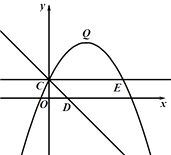
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
参考答案:
【答案】
(1)解:设抛物线的解析式为 ![]() ,
,
将C(0,1)代入得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为: ![]() 即
即 ![]()
(2)解: ①如图1,当点C为直角顶点时,
∵点C的坐标为(0,1),
∴OD=OC=1,
∴点D的坐标为(1,0),
设直线CD为 ![]() ,则:
,则: ![]() ,解答
,解答 ![]() ,
,
∴直线CD的解析式为: ![]() ,
,
∵此时CM⊥CD,
∴CM的解析式为: ![]() ,
,
由: 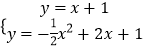 ,解得:
,解得: ![]() ,
, ![]() ,
,
∵点(0,1)与点C重合,
∴点M的坐标为(2,3),此时点M与点Q重合;
②如图②,当D为直角顶点时,由①可得直线DM的解析式为 ![]() ,
,
由:  ,解得:
,解得: ![]() ,
, ![]() ,
,
∴点M的坐标为为 ![]() 或
或 ![]() ;
;
综上所述,符合题意的M有三点,分别是(2 , 3 ), ![]() 或
或 ![]() .
.
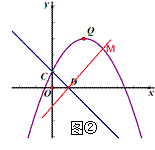
(3)解:存在.如图③所示,作点C关于直线QE的对称点C′,作点C关于x轴的对称点C″,连接C′C″,交OD于点F,交QE于点P,则△PCF即为符合题意的周长最小的三角形,由轴对称的性质可知,△PCF的周长等于线段C′C″的长度.
如答图④所示,连接C′E,
由(2)可知,QC⊥CD, 由题意可得:QC=QE,
∵∠DCE=45°,
∴∠QCE=45°=∠QEC,
∴△QCE是等腰直角三角形,
∵C,C′关于直线QE对称,
∴△QC′E为等腰直角三角形,
∴△CEC′为等腰直角三角形,
∵在抛物线 ![]() 中,由
中,由 ![]() 解得
解得 ![]() ,
,
∴点E的坐标为(4,1),
∴CE=4=C′E,
∴点C′的坐标为(4,5);
∵C,C″关于x轴对称,
∴点C″的坐标为(0,﹣1).
∴OC″=1,
过点C′作C′N⊥y轴于点N,则NC′=CE=4,NC″=4+1+1=6,
在Rt△C′NC″中,由勾股定理得:C′C″= ![]() .
.
综上所述,在P点和F点移动过程中,△PCF的周长存在最小值,最小值为 ![]() .
.
【解析】(1)解析式可设为顶点式,再把C(0,1)代入解析式即可;(2)以CD为直角边的直角三角形分为两类,分别以C、D为直角顶点,可过C、D分别作CD的垂线,与抛物线相交,联立直线和抛物线解析式组成方程组,可求出M坐标;(3)可利用对称法作出C关于定直线QE的对称点C',关于y轴对称点为C",把△PCF的周长转化为FC"+FP+PC',当C"、F、P、C'四点共线时,周长最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E.请完成解答过程.
证明:∵AD∥BE(已知)
∴∠A=∠ ( )
又∵∠1=∠2(已知)
∴AC∥ ( )
∴∠3=∠ (两直线平行,内错角相等)
∴∠A=∠E(等量代换)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).
(1)求w与x之间的函数关系式;
(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该商品,商场销售新产品,每月的销量与销售价格之间的关系与原产品的销售情况相同,新产品的成本每件32元,若新产品每月的销售量不低于200件时,政府部门给予每件4元的补贴,试求定价多少元时,每月销售新产品的利润最大?求出最大的利润。 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个数的平方等于
 ,记为
,记为  ,这个数
,这个数  叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为  (
(  为实数),
为实数),  叫这个复数的实部,
叫这个复数的实部,  叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: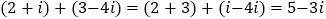
(1)填空: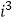 = ,
= ,  = .
= .
(2)填空:① ; ②
; ②  .
.
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ,(
,(  为实数),求
为实数),求  的值.
的值.
(4)试一试:请利用以前学习的有关知识将 化简成
化简成  的形式.
的形式.
(5)解方程:x2 - 2x +4 = 0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A(m,0),B(n,0),C(﹣1,2),且满足式|m+2|+(m+n﹣2)2=0.
(1)求出m,n的值.
(2)①在x轴的正半轴上存在一点M,使△COM的面积等于△ABC的面积的一半,求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使△COM的面积等于△ABC的面积的一半仍然成立,若存在,请直接在所给的横线上写出符合条件的点M的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE,当点P运动时,
 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是数a,b,c,d,且d-2a=10,那么数轴的原点应是( )

A.点A
B.点B
C.点C
D.点D
相关试题

