【题目】已知直线l1∥l2 , 点A是l1上的动点,点B在l1上,点C、D在l2上,∠ABC,∠ADC的平分线交于点E(不与点B,D重合).
(1)若点A在点B的左侧,∠ABC=80°,∠ADC=60°,过点E作EF∥l1 , 如图①所示,求∠BED的度数. 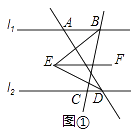
(2)若点A在点B的左侧,∠ABC=α°,∠ADC=60°,如图②所示,求∠BED的度数;(直接写出计算的结果) 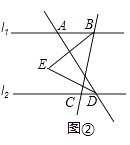
(3)若点A在点B的右侧,∠ABC=α°,∠ADC=60°,如图③所示,求∠BED的度数. 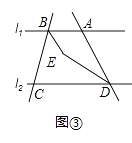
参考答案:
【答案】
(1)解:∵BE、DE分别是∠ABC,∠ADC的平分线,
∴∠ABE= ![]() ∠ABC=
∠ABC= ![]() ×80°=40°,∠CDE=
×80°=40°,∠CDE= ![]() ∠ADC=
∠ADC= ![]() ×60°=30°.
×60°=30°.
∵EF∥L1,
∴∠BEF=∠ABE=40°.
∵L1∥L2
∴EF∥L2
∴∠DEF=∠CDE=30°
∴∠BED=∠BEF+∠DEF=40°+30°=70°
(2)解:BE、DE分别是∠ABC,∠ADC的平分线,
∴∠ABE= ![]() ∠ABC=
∠ABC= ![]() α°,∠CDE=
α°,∠CDE= ![]() ∠ADC=
∠ADC= ![]() ×60°=30°.
×60°=30°.
∵EF∥L1,
∴∠BEF=∠ABE= ![]() α°.
α°.
∵L1∥L2,
∴EF∥L2,
∴∠DEF=∠CDE=30°
∴∠BED=∠BEF+∠DEF= ![]() α°+30°,即∠BED=(
α°+30°,即∠BED=( ![]() α+30)°
α+30)°
(3)解:过点E作EF∥L1,
∵BE,DE分别是∠ABC、∠ADC平分线,
∴∠ABE= ![]() ∠ABC=
∠ABC= ![]() α°,∠CDE=
α°,∠CDE= ![]() ∠ADC=
∠ADC= ![]() ×60°=30°.
×60°=30°.
∵EF∥L1,
∴∠BEF=(180﹣ ![]() α)°.
α)°.
又∵L1∥L2
∴EF∥L2
∴∠DEF=∠CDE=30°
∴∠BED=∠BEF+∠DEF
=(180﹣ ![]() α+30)°
α+30)°
=(210﹣ ![]() α)°
α)°
【解析】(1)根据BE、DE分别是∠ABC,∠ADC的平分线,得出∠ABE= ![]() ∠ABC,∠CDE=
∠ABC,∠CDE= ![]() ∠ADC,再由平行线的性质得出∠BEF=∠ABE,同理可得出∠DEF=∠CDE,再由∠BED=∠BEF+∠DEF即可得出结论;(2)过点E作EF∥AB,同(1)的证明过程完全相同;(3)过点E作EF∥L1 , 根据BE,DE分别是∠ABC、∠ADC平分线可知∠ABE=
∠ADC,再由平行线的性质得出∠BEF=∠ABE,同理可得出∠DEF=∠CDE,再由∠BED=∠BEF+∠DEF即可得出结论;(2)过点E作EF∥AB,同(1)的证明过程完全相同;(3)过点E作EF∥L1 , 根据BE,DE分别是∠ABC、∠ADC平分线可知∠ABE= ![]() ∠ABC=
∠ABC= ![]() α°,∠CDE=
α°,∠CDE= ![]() ∠ADC,再由EF∥L1可知∠BEF=(180﹣
∠ADC,再由EF∥L1可知∠BEF=(180﹣ ![]() α)°.根据L1∥L2可知EF∥L2 , 故∠DEF=∠CDE=30°,所以∠BED=∠BEF+∠DEF.
α)°.根据L1∥L2可知EF∥L2 , 故∠DEF=∠CDE=30°,所以∠BED=∠BEF+∠DEF.
【考点精析】本题主要考查了平行线的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦BC长为
 ,弦AC长为2,∠ACB的平分线交⊙O于点D,
,弦AC长为2,∠ACB的平分线交⊙O于点D,
(1)求AD的长.
(2)求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
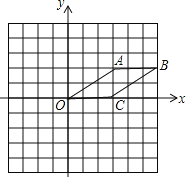
(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是__________.
(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2;连接OB,求出OB旋转到OB2所扫过部分图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某存计划建造
 、
、 两种型号的沼气池共
两种型号的沼气池共 个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
已知可供建造沼气池的占地面积不超过
 ,该村农户共有
,该村农户共有 户.
户.(
 )满足条件的方案共有几种?写出解答过程.
)满足条件的方案共有几种?写出解答过程.(
 )通过计算判断,哪种建造方案最省钱.
)通过计算判断,哪种建造方案最省钱. -
科目: 来源: 题型:
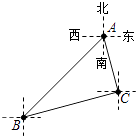
查看答案和解析>>【题目】如图,B处在A处的西南方向,C处在A处的南偏东15°方向,若∠ACB=90°,则C处在B处的( )
A.北偏东75°方向
B.北偏东65°方向
C.北偏东60°方向
D.北偏东30°方向 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a3+a4=a7B. a4a5=a9C. 4m5m=9mD. a3+a3=2a6
相关试题

