【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
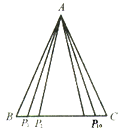
A. 4 B. 14 C. 40 D. 不能确定
参考答案:
【答案】C
【解析】
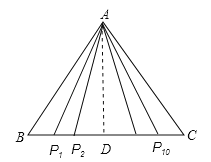
作AD⊥BC于D.根据勾股定理,得APi2=AD2+DPi2=AD2+(BD﹣BPi)2=AD2+BD2﹣2BDBPi+BPi2,PiBPiC=PiB(BC﹣PiB)=2BDBPi﹣BPi2,从而求得Mi=AD2+BD2,即可求解.
作AD⊥BC于D,则BC=2BD=2CD.
根据勾股定理,得:
APi2=AD2+DPi2=AD2+(BD﹣BPi)2=AD2+BD2﹣2BDBPi+BPi2,
又PiBPiC=PiB(BC﹣PiB)=2BDBPi﹣BPi2,
∴Mi=AD2+BD2=AB2=4,∴M1+M2+…+M10=4×10=40.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,底边BC为2
 ,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( )
,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为( ) 
A.2+2
B.2+
C.4
D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品 20 袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:

①这批样品的平均质量比标准质量多还是少?用你学过的方法合理解释;
②若标准质量为 450 克,则抽样检测的总质量是多少?
-
科目: 来源: 题型:
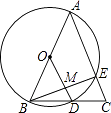
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10,以AB为直径的⊙O与BC交于点D,与AC交于点E,连OD交BE于点M,且MD=2,则BE长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中
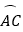 的长是cm(计算结果保留π).
的长是cm(计算结果保留π).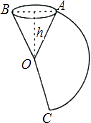
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC=2
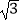 ,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB= .
,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,B点恰好落在对角线AC上的B′处,则AB= .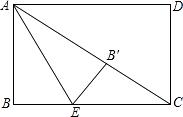
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
相关试题

