Question

【题目】在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．

（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=3，AB=4，求菱形ADCF的面积．

Answer 1

【答案】
（1）证明：①∵AF∥BC，
∴∠AFE=∠DBE，
∵E是AD的中点，AD是BC边上的中线，
∴AE=DE，BD=CD，
在△AFE和△DBE中，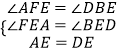
，
∴△AFE≌△DBE（AAS）
（2）证明：由（1）知，△AFE≌△DBE，则AF=DB．
∵DB=DC，
∴AF=CD．
∵AF∥BC，
∴四边形ADCF是平行四边形，
∵∠BAC=90°，D是BC的中点，E是AD的中点，
∴AD=DC= BC，
∴四边形ADCF是菱形
（3）解：连接DF，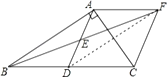

∵AF∥BD，AF=BD，
∴四边形ABDF是平行四边形，
∴DF=AB=4，
∵四边形ADCF是菱形，
∴S菱形ADCF= ACDF= ×3×4=6．
【解析】（1）根据平行线的性质证明∠AFE=∠DBE，再根据中点的定义及三角形中线的定义证明AE=DE，BD=CD，然后利用三角形全等的判定定理证明△AEF≌△DEB即可。
（2）根据（1）的结论及已知先证四边形ADCF是平行四边形，再利用直角三角形斜边上的中线等于斜边的一半证明AD=DC，然后根据一组邻边相等的平行四边形是菱形，即可证得结论。
（3）连接DF，易证四边形ABDF是平行四边形，就可求出DF的长，再根据菱形的面积等于两对角线之积的一半，求得菱形的面积即可。