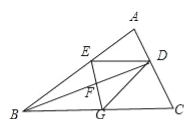
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
参考答案:
【答案】(1)四边形EBGD是菱形,理由见解析;(2)![]() .
.
【解析】
试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
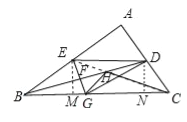
在△EFD和△GFB中,
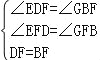 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2![]() ,
,
∴EM=![]() BE=
BE=![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=![]() ,MN=DE=2
,MN=DE=2![]() ,
,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=![]() ,
,
∴MC=3![]() ,
,
在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=3
.MC=3![]() ,
,
∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,表示甲、乙两同学沿同一条路到达目的地过程中,路程S(千米)与时间t(小时)之间关系的图象,根据图象中提供的信息回答问题:
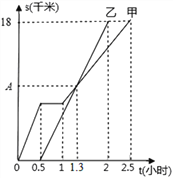
(1)乙的速度为_______千米/时;
(2)两人在乙出发后________小时相遇;
(3)点A处对应的数字为_________;
(4)甲在出发后1小时至2.5小时之间的速度为_________千米/时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)物体向右运动4m记作+4m,那么物体向左运动3m,应记作____m.
(2)单项式﹣
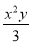 的系数是____.
的系数是____.(3)一个数的倒数是﹣1,这个数是____.
(4)|a|=5,|b|=3,且|a+b|=a+b,则ab=____.
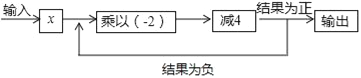
(5)按下列程序输入一个数x,若输入的数x=0,则输出结果为____.
(6)如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
 ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为__________________.
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为__________________. 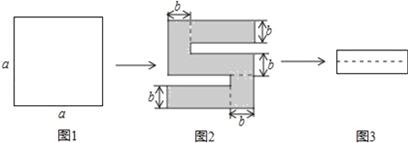
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
十进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例如,用十六进制表示:C+F=1B,19﹣F=A,18÷4=6,则A×B=( )
A. 72 B. 6E C. 5F D. B0
-
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB经过平移得到线段CD,若CD=5cm,则AB等于( )
A.3cm
B.4cm
C.5cm
D.6cm -
科目: 来源: 题型:
查看答案和解析>>【题目】等式的性质:
(1)等式两边加(或减)同一个________(或________),结果仍相等.用字母表示:如果a=b,那么a±c=b________;
(2)等式两边乘同一个________,或除以同一个________,结果仍相等.用字母表示:如果a=b,那么ac=________;如果a=b(c≠0),那么
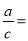 _________.
_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填在相应的集合里。
—3.8, -20%, 4.3, —∣—
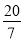 ∣, 42, 0, —(—
∣, 42, 0, —(—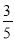 ),
), 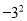
整数集合:{ … };
分数集合:{ … };
正数集合:{ … };
负数集合:{ … }。
在已知的数据中,最大的数是 ,最小的数是 .
相关试题

